What is Break-Even Analysis?
At startup, founders and owners have a keen interest in knowing the break-even point—what it will take to start making profits.
Break-even Analysis sddresses questions like these:
- How many product units must we sell to break even?
- How many rooms must we rent to cover costs?
- At what level of sales revenues do we become profitable?
Define Break Even
The term Break-Even Point refers to the exact business volume at which total cash outflows equals total cash inflows. For this reason, the break-even point is also called Break-Even Volume. At break-even, net cash flow equals zero.
Break-even analysis is a methodology for finding break-even volume by analyzing relationships among fixed and variable costs, business volume, pricing, and net cash flow. For analysis purposes, Business Volume usually means a measure of (1) unit sales or (2) sales revenues.
The term break even is a verb, as in "When do we break even?" The form break-even is an adjective, as in "The break-even point." However, it is also correct to spell both the verb and the adjective as breakeven.


The Break-Even Concept
Break-even analysis attempts to find break-even volume by analyzing relationships among fixed and variable costs, business volume, pricing, and net cash flow. Understanding how these factors impact each other is crucial in budgeting, production planning, and profit forecasting, Break-even analysis, is central to this understanding.
The essential components of simple break-even analysis include:
- Cash inflows (or revenues).
- Fixed costs.
- Variable costs.
- Semi-variable costs (sometimes).
Cash inflows
The simple analysis assumes that each unit brings the same cash inflow. For sellers, cash inflow per unit is the same as the selling price per unit.
Fixed costs
Fixed costs remain fixed, or constant, regardless of unit volume. For example, if the floor space expenses, manager's salaries, and janitorial services, do not change with unit volume, they are fixed costs.
Variable costs
These costs vary in direct proportion to quantity sold or unit volume. Variable costs for selling goods, for instance, might include the "direct cost" the seller pays to acquire each unit. As a result, the total variable cost can be "cost per unit" multiplied by the unit volume.
Semi-variable costs
Semi-variable costs are constant across a range of business volumes, but change when that volume goes out of range. Wages for a call center operator, for example, might be a fixed cost when daily call volume is between 0 and 100 calls per day. A second operator might be necessary when call volume is 101 to 200. And, a third might be required if daily call volume is 201 to 300.
- Within each call volume range (e.g., 201-300), operator cost is fixed.
- Across all ranges (0 - 300), operator cost is semi-variable.
Break-Even Point as Unit Volume
In business, the break-even point usually means the unit volume that balances total costs with total gains. For the analyst, Break-Even is the quantity Q for which cash outflows equal cash inflows, exactly. At the break-even quantity, therefore, net cash flow equals zero.
The Simple break-even analysis finds Q by analyzing relationships between just three variables: fixed costs, variable costs, and cash inflows. The analyst must consider additional factors, however, when semi-variable costs or variable pricing are present.
Break-Even Point as a Timespan
Note that businesspeople also refer to a similar but different concept, the break-even point in time, or payback period. Payback period is the time necessary for investment returns to cover investment costs. Payback analysis does not consider units, but instead the timing of cash inflows and outflows. For more on the break-even point in time, see Payback period.
Break-even points for Business Startup
businesspeople starting a new business need especially to understand both kinds of break-even points (break-even time and break-even unit volume). They must understand both because startups typically lose money for a while before becoming profitable. There is a limit, however, to the time owners can tolerate losses. Before launching a new business, therefore, they have a keen interest in knowing the break-even business volume. The new firm turns profitable only when business volume exceeds "break-even volume." A decision to launch the business may depend on the owners' view of the time and expense required to reach that volume.
Explaining Break-Even in its Context
Sections below further define, describe and illustrate break-even analysis. Note that the term appears in context with related terms and concepts from the fields of business analysis, finance, and investment analysis.
Contents
- What is a break-even point analysis?
- What is "simple Break-Even?"
- How do you find a break-even point with a graphical solution?
- How do you calculate Break-Even with semi-variable cost figures?
- How does break-even analysis change with variable pricing or other variable inflows?
Related Topics
- Payback period: The break-even point in time. See Payback Period.
- Introduction to financial metrics--cash flow metrics and financial statement metrics. See Financial Metrics.
What is Simple Break-Even?
Simple Break-Even Analysis addresses questions of this kind: How many units must we sell to Break-Even? That is, How many units must we sell to bring total cash inflows equal total cash outflows?
The symbol for the answer is Q. The value of Q is the number of units that exactly balances cash inflows with cash outflows—the Break-Even point.
How to Calculate Simple Break Even in 4 Steps
Formulas and Example Calculations
The simple form of break-even analysis considers just three input variables:
Step 1 Specify Input Variable 1, Cash Inflow Per Unit (P)
For sellers, cash inflow per unit usually means the unit selling price per unit, with symbol P. As a result, analysts sometimes label this variable as revenues. The cash inflow total, therefore, is a function of unit volume.
Step 2. specificity Input Variable 2, Total Fixed Cost (F)
These costs are constant across all possible unit volumes. Example "fixed costs" include such things as equipment costs, floor space leasing costs, and executive staff salaries. The symbol F stands for Total fixed costs.
Step 3. Specify Variable Cost Per Unit (v)
The variable cost total varies by unit volume. Typical variable costs include per unit costs for such things as factory direct labor, materials, and sales commissions.
Step 4. Calculate Breakeven Quantity Q with the Simple Breakeven Formula.

The formula finds the break-even number of units—break-even point—as follows:
Q = (1,200) / (40 – 15)
= 1,200 / 25
= 48 units
Knowing the break-even quantity Q, the analyst verifies the result by comparing total inflows total outflows using the formula above
Total Inflows
= Q * P = (48) ( $40) = $1,920
Total Costs
= Fixed costs + Variable costs
= F + (Q * v) = $1,200 + (48)($15) = $1,920
Sometimes the break-even result includes a fractional unit (for example, 50.34 units). No one sells or ships fractional units, however. In such cases, of course, the analyst rounds break-even quantity Q up to the next whole unit (to 51 units).
Break-Even Point Does Not Exist When Selling at a Loss
Naturally, break-even point Q does not exist for products selling at a loss. These products produce a negative gross margin because the unit cost of goods sold is higher than the unit selling price.
There are in fact a few strategic reasons for selling one or a few products at a loss. Sellers may use a "loss leader," for example, simply to "get customers into the store," or to leverage sales of other products. And, they may sell at a loss to pursue rapid market share gains. Such products, however, always contribute a net loss to profits, regardless of volume.
Finding Break-Even Point With a Graphical Solution
Illustrated Example
Finding a break-even point with a formula is a simple task. Finding the break-even point with a graphical solution requires more time and effort, and not many people seeking a single point solution will resort to the graphical approach. However, the graphical approach is indispensable when using break-even metrics in business planning or business case analysis results.
For planning and analysis purposes, the analyst plots graphic data such as Exhibit 2, produced by a spreadsheet-model that turns input data assumptions into breakeven results. Spreadsheet and graph used this way enable:
- Extensive "What if?" testing
The visual display reveals very clearly the impact of changing input values on break-even point, and on total costs and total earnings.1 - Risk analysis
Build confidence interval estimates for the range and probabilities of different break-even point results. 2 -
Sensitivity Analysis
Measure sensitivity of estimated break-even points to changes in the input assumptions (variable cost per unit, selling price per unit, and fixed cost.2
Exhibit 2 shows the net cash flow result (solid black line) due to the different values of the input variables (selling price, fixed costs, variable costs, and unit volume).
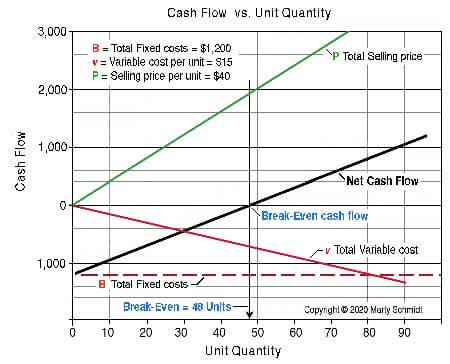
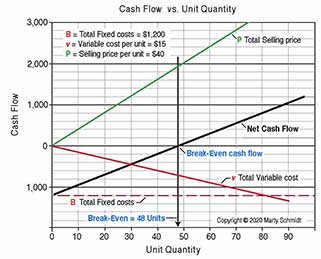
Exhibit 2. Break-even occurs at the Unit Quantity under the point where the Net Cash Flow line crosses the vertical axis "0" cash flow line.
The four plotted ines on the graph show the resulting vertical axis values as a function of horizontal axis unit quantity. Because the break-even equation is a linear equation, all four "curves" graph as straight-lines. The graph, in other words, plots unit volume (v) as an independent variable, along with results for three dependent variables:
- Variable costs
- Fixed costs
- Net cash flow
The "Net Cash Flow" curve is, in fact, the difference between net inflows and net outflows. For graphing purposes, net cash flow for any unit volume UVi calculates as:
Net cash flow at UVi
= (UVi * Cash inflow per unit)
– (Variable costs at UVi + Fixed costs)
As unit volume increases, net cash flow climbs from negative to positive. And, as a result, break-even quantity Q is the unit volume where net cash flow crosses 0 on the horizontal axis.
__________________________
1. For working spreadsheet examples of the break-even equation and break-even graphs, as they appear above, see the Excel-based ebook Financial Metrics Pro.
2. For an introduction to rmodel-based risk and sensitivity analysis, see the article Risk and Sensitivity Analysis for the Business Case.
Calculating Break-Even With Semi-Variable Costs
In the simple example above, the total variable cost is the product of unit volume and "unit cost." This approach is correct, because "unit cost" is constant across all unit volumes.
The analyst faces new complexities, however, when "unit cost" itself also changes with unit volume. As a result, "Variable cost" in the break-even analysis is not a simple linear function of unit volume. This situation occurs in business, where, for instance:
- The manufacturer's unit cost for raw materials depends on the size of the raw materials order.
- Direct labor costs per unit may depend somewhat on the size of the production run. Consequently, labor cost per unit differs for different volumes.
- Above a specific unit volume, a company may have to add more staff or production equipment. These additional costs may be "fixed costs" within a limited volume range, but across all such spans, they are semi-variable costs.
- Companies that want to achieve high unit volume may have to lower selling price, or offer volume discounts, or use pricing tiers for different order sizes. As a result, not all units sell at the same price. In this case, the result is semi-variable inflows.
Under such conditions, the simple break-even equation is not accurate, or else it is accurate only within a limited range of unit volumes.
Example Break-Even With semi-variable Costs
Consider a manufacturing setting with three cost and price factors:
B = Total Fixed costs = $1,200
v
= Variable cost per unit = $15
P
= Selling price per unit = $40
Now, however, there is an additional semi-variable cost factor (sv). When production volume is 0 - 30 units, an additional $100 labor cost is required, making sv1 = $100. For volumes in the range 31-60 units, additional labor costs are $200 meaning that sv2 = $200. In the range 61-90 units, additional labor costs are $300 meaning that sv2 = $300. Exhibit 3 below summarizes this semi-variable cost factor.
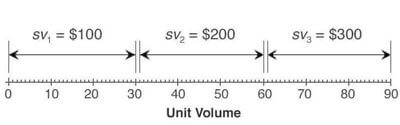
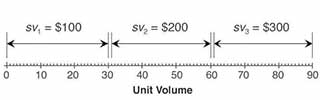
Finding Break-Even With Semi-Variable Costs
The most straightforward approach to calculating the break-even volume is to use the simple equation separately for each range. Consequently, total fixed costs in each range "i" are the sum of the given overall fixed cost (F) and the semi-variable cost for the span "svi."
Step 1. Finding Fixed Costs For Each Range
Total fixed cost for range i = F+svi.
Step 2 Finding Ranges Containing Break-Even
The next step is to find which spans, if any, contain a break-even point. Depending on the input figures, it is possible to have no ranges with a break-even point, or break-even in just one span, or break-even points multiple spans.
- When a unit volume range shows net cash flow negative at one point and positive at another, the range includes a break-even point.
- If net cash flow is negative throughout the range or positive throughout, the span does not include a break-even point.
To test these two criteria for this example, we need only calculate net cash flow at the lower limit and upper limit. These two calculations suffice for calculating cash flow across each range is a linear function of unit volume. That is, net cash flow is a "straight-line" function.
Example Calculations With Semi-Variable Costs
For this example, we can determine if each range span has a break-even point by calculating net cash flow at its upper and lower limits using this equation:
Net cash flow = Incoming cash flow – Range total fixed cost – Variable cost
= Units * P − (F+svi )– Units * v
Breakeven for Range 1 (0 - 30 units)
Examine Range 1 for possible break-even points with these calculations:
Net cash flow at 0 units
= (0)( $40 ) −( $1,200 + $100 ) − ( 0 ) ($15 ) = −$1,300
Net cash flow at 30 units
= (30)( $40 ) − ( $1,200 + $100 ) − ( 0 ) ($15 ) = −$550
Conclusion 1:
Range 1 has no break-even points because net cash flow is negative across the entire range.
Breakeven for Range 2 (31 - 60 units)
Examine Range 2 for possible break-even points with these calculations:
Net cash flow at 31 units
= (31)( $40 ) −( $1,200 + $200 ) − ( 31 ) ($15 ) = −$625
Net cash flow at 60 units
= (60)( $40 ) − ( $1,200 + $200 ) − ( 60 ) ($15 ) = $100
Conclusion 2:
Range 2 has a break-even point because net cash flow is negative at the range lower limit (31 units) and positive at the upper limit (60 units). Within this range, therefore, semi-variable costs sv2 are constant and thus add into fixed costs, F. As a result, the analyst finds the Range 2 break-even point with the break-even formula Q = F/ ( P - v ), applying it to this range only.Break-even ( Q ) in Range 2 = ( $1,200 + $200 ) / ($40 – $15) = 56 units
Breakeven for Range 3 (61-90 units)
Examine Range 3 for possible break-even points with these calculations:
Net cash flow at 61 units
= (61)( $40 ) −( $1,200 + $300 ) − ( 61 ) ($15 ) = $25
Net cash flow at 90 units
= (90)( $40 ) − ( $1,200 + $300 ) − ( 90 ) ($15 ) = $750
Conclusion 3:
Range 3 does not have a break-even point because all unit volumes in the range show positive net cash flow. All unit volumes in the range are therefore above Break-Even.
For more on semi-variable costs in break-even analysis, and working spreadsheet example, see Financial Metrics Pro.
How Does Break-Even Analysis Change With Variable Inflows?
Variable Inflow Sources
The analysis in the examples above assumes constant cash inflow (or selling price, P) for each unit sold. However, in some situations, different customers pay different prices for the same goods or services.
- Seats on airline flights often sell at different prices. Airline ticket price may depend on such things as the class of service, advance purchase, demand for the day, or competitor's prices. And, sometimes, they offer only a few seats at discount prices.
- Consultants, physicians, and other professional service providers sometimes charge clients according to their willingness or ability to pay.
- Businesses that sell to other companies may negotiate prices individually with each customer.
- Companies launching new products or entering new markets may try out different pricing models from time to time.
Calculating Break-Even With Variable Inflows
Break-even questions still have relevance in such cases. However, cash inflows that can vary from unit to unit call for an analysis that is more complex than the examples shown above.
In such cases, the break-even analyst can proceed as follows:
- Firstly, find break-even quantity using an average (mean) inflow or average (mean) selling price per unit. This analysis shows the cash inflow total that balances costs, that is, to breaks even
- Secondly, set this cash inflow level as a target to reach for Break-Even.
- Thirdly, propose different pricing models and their resulting unit volume needs for reaching the target inflow.

