The Meaning of Discounted Cash Flow (DCF), Net Present Value (NPV), and Related Time Value of Money Concepts

Encyclopedia of Business Terms and Methods, ISBN 978-1-929500-10-9. Revised 2013-05-03.

Discounted Cash Flow (DCF) is a cash flow summary adjusted so as to reflect the time value of money. With discounting, money to be received or paid at some time in the future is viewed as having less value, today, than than an equal amount that is received or paid today. This item defines, explains, and illustrates the following terms with examples:

• Present value (PV) is what the future cash flow is worth today.
• Future value (FV) is the value, in non discounted currency units that actually flows in or out at the future time. A $100 cash inflow that will arrive two years from now could, for example, have a present value today of about $94, while its future value is still considered $100.
• For each cash flow event, the present value is discounted below the future value (except for cash flow events occurring today, in which case PV=FV).
• The longer the time period before an actual cash flow event occurs, the more the present value of future money is discounted below its future value.
• The total discounted value (present value) for a series of cash flow events across a time period extending into the future is known as the net present value (NPV) of a cash flow stream. 

DCF can be an important factor when evaluating or comparing investments, proposed actions, or purchases. Other things being equal, the action or investment with the present value after discounting is the better decision. When discounted cash flow events in a cash flow stream are added together, the result is called the net present value (NPV).

DCF and NPV and related time value of money concepts are more easily understood when explained together and illustrated, along with related concepts such as discount rate, future value (FV), and present value (PV), as shown in the sections below.

• Time value of money in finance and business planning
• Present value, future value, and net present value  
• DCF and NPV: Mathematically speaking  
• Choosing a discount Rate for discounted cash flow analysis  
• NPV DCF example: comparing competing investments with NPV  
• When to use discounting and NPV in the business case

Time value of money in finance and business planning

When business case or investment projections extend more than a year into the future, professionals trained in finance usually want to see cash flows in both discounted terms and non discounted terms. They want to see projections, that is, that consider the time value of money. In modern finance, time-value-of-money concepts play a central role in decision support and planning.

Time value of money analysis begins with the present value concept, the idea that money you have now is worth more, today, than an identical amount you would receive in the future Why? There are at least 3 reasons:

• Opportunity. The money you have now you could (in principle) invest now, and gain return or interest, between now and the future time. Money you will not have until a future time cannot be used now. 
• Risk. Money you have now is not at risk. Money predicted to arrive in the future is less certain.
• Inflation. A sum you have today will very likely buy more than an equal sum you will not have until years in future. Inflation over time reduces the buying power of money.

Present value, future value, and net present value

What future money is worth today is called its present value (PV), and what it will be worth in the future when it finally arrives is called not surprisingly its future value (FV). The right to receive a payment one year from now for $100 (the future value) might be worth to us today $95 (its present value). Present value is discounted below future value.

When the analysis concerns a series of cash inflows or outflows coming at different future times, the series is called a cash flow stream. Each future cash flow has its own value today (its own present value). The sum of these present values is the net present value for the cash flow stream. 

Consider an investment today of $100, that brings net gains of $100 each year for 6 years. The future values and present values of these cash flow events might look like this:

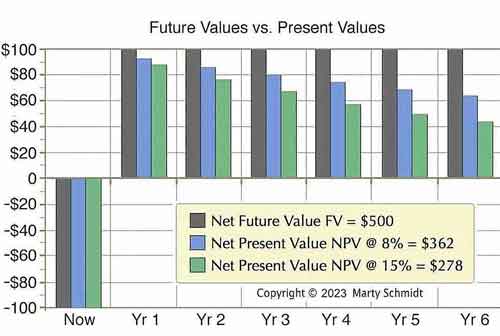
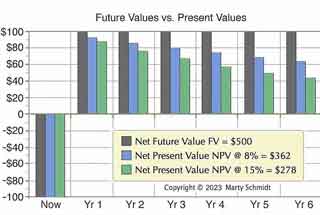
All three sets of bars represent the same investment cash flow stream. The black bars stand for cash flow figures in the currency units when they actually appear in the future (future values). The lighter bars are values of those cash flows now, in present value terms. The net values in the legend show that after five years, the net cash flow expected is $500, but the Net present value today is discounted to something less.

The size of the discounting effect depends on two things: the amount of time between now and each future payment (the number of discounting periods)  and an interest rate called the discount rate. The example shows that:

• As the number of discounting periods between now and the cash arrival increases, the present value decreases.
• As the discount rate (interest rate) in the present value calculations increases, the present value decreases. 

Whether you will or will not calculate present values yourself, your ability to use and interpret NPV / DCF figures will benefit from a simple understanding of the way that interest rates and discounting periods work together in discounting. If you wish to skip the next section on mathematics, however, click here to skip the maths topic and go directly to  "Choosing a Discount Rate."

DCF and NPV: Mathematically speaking

DCF and NPV calculations are closely related to calculations for interest growth and compounding, which are already familiar to most people. Remember briefly how these work. The formula at left looks into the future and might ask, for instance: What is the future value (FV) in one year, of $100 invested today (the PV), at an annual interest rate of 5%?

FV₁  = $100 ( 1 + 0.05)¹ = $105

When the FV is more than one period into the future, as most people know, interest compounding takes place. Interest earned in earlier periods begins to earn interest on itself, in addition to interest on the original PV. Compound interest growth is delivered by the exponent in the FV formula, showing the number of periods. What is the future value in five years of $100 invested today at an annual interest rate of 5%?

FV₅  = $100 ( 1 + 0.05)⁵ = $128

The same formula can be rearranged to deliver a present value given a future value and interest rate for input, as shown at left. Now, the formula starts in the future and looks backwards in time, to today, and might ask: What is the value today of a $100 payment arriving in one year, using a discount rate of 5%?

PV₁ = ($100) / (1.0 + 0.05)¹     = $100 / (1.05)     = $95 

You should be able to see why PV will decrease if we either (a) increase the interest rate, or (b) increase the number of periods before the FV arrives. What is the present value of $100 we will receive in 5 years, using a 5% discount rate?

PV₅  = $100 / (1.0 +0.05)⁵      = $100 / (1.276)     = $75.13

When discounting is applied to a series of cash flow events, a cash flow stream, as illustrated in the graph example above, net present value for the stream is the sum of PVs for each FV:

Finally, note two commonly used variations on the examples shown thus far. The examples above and most textbooks show  "year end" discounting, with periods one year in length, and cash inflows and outflows discounted as though all cash flows in the year occur on day 365 of the year. However:

• Some financial analysts prefer to assume that cash flows are distributed more or less evenly throughout the period, and discounting should be applied when the cash actually flows.
• For calculating present values this way, it is mathematically equivalent to calculate as though all cash flow occurs at mid year.  This is so-called "mid period discounting." 
• Year end discounting is more severe (has a greater discount effect) than mid year (mid period) discounting, because the former discounts all cash flow in the period for the full period.
• When actual cash flow is known or estimated for months, quarters, or some other period, discounting may be performed for each of these periods rather than for one year periods. In such cases, the discount rate used for calculation is the annual rate divided by the fraction of a year covered by a period. Quarterly discounting, for example, would use the annual rate divided by 4.

The formulas at left show NPV calculations for mid-year discounting (upper formula) and for discounting with periods other than one year (lower formula).

In any case, the business analyst will want to find out which of the above discount methods is preferred by the organization's financial specialists, and why, and follow their practice (unless there is justification for doing otherwise).

Working examples of these formulas, along with guidance for spreadsheet implementation and good-practice usage are available in the spreadsheet-based tool Financial Metrics Pro.

Choosing a discount rate for discounted cash flow analysis

The analyst will also want to find out from the organization's financial specialists which discount rate the organization uses for discounted cash flow analysis. Financial officers who have been with an organization for some time, usually develop good reasons for choosing one rate or another as the most appropriate rate for the organization.

• In private industry, many companies use their own cost of capital (or weighted average cost of capital) as the preferred discount rate.
• Government organizations typically prescribe a discount rate for use in the organization's planning and decision support calculations. In the United States, for instance, the Office of Management and Budget (OMB) publishes a quarterly circular with prescribed discount rates for Federal Government use.
• Financial officers may use a higher discount rate for investments or decisions viewed as risky, and a lower discount rate when expected returns from a proposed action are seen as less risky.  The higher rate is viewed as a hedge against risk, because it puts relatively more emphasis (weight) on near-term returns compared to distant future returns.

Example: Comparing competing investments with NPV.

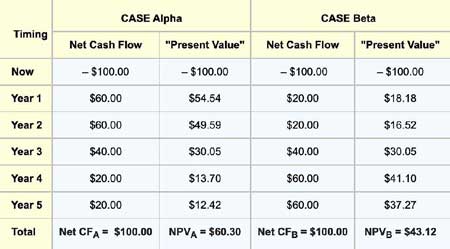
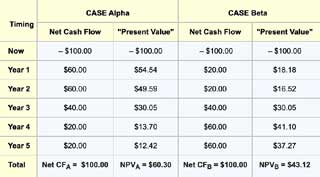
Consider two competing investments in computer equipment. Each calls for an initial cash outlay of $100, and each returns a total a $200 over the next 5 years making net gain of $100. But the timing of the returns is different, as shown in the table below (Case A and Case B), and therefore the present value of each year’s return is different. The sum of each investment’s present values is called the discounted cash flow (DCF) or net present value (NPV). Using a 10% discount  rate again, we find:

Timing	CASE A		CASE B
	Net Cash Flow	Present Value	Net Cash Flow	Present Value
Now	– $100.00	– $100.00	– $100.00	– $100.00
Year 1	$60.00	$54.54	$20.00	$18.18
Year 2	$60.00	$49.59	$20.00	$16.52
Year 3	$40.00	$30.05	$40.00	$30.05
Year 4	$20.00	$13.70	$60.00	$41.10
Year 5	$20.00	$12.42	$60.00	$37.27
Total	Net CFA =  $100.00	NPVA = $60.30	Net CFB = $100.00	NPVB = $43.12

Comparing the two investments, the larger early  returns in Case A lead to a better net present value (NPV) than the later large returns in Case B. Note especially the Total line for each present value column in the table. This total is the net present value (NPV) of each "cash flow stream." When choosing alternative investments or actions, other things being equal, the one with the higher NPV is the better investment.

When to use discounting and NPV in the business case

In brief, an NPV / DCF view of the cash flow stream should probably appear with a business case summary when:

• The business case deals with an "investment" scenario of any kind, in which different uses for money are being compared.
• The business case covers long periods of time (two or more years).
• Inflows and outflows change differently over time (e.g., the largest inflows come at a different time from the largest outflows).
• Two or more alternative cases are being compared and they differ with respect to cash flow timing within the analysis period.

For a working spreadsheet example of discounted cash flow calculations, download either the free financial metrics tool (click here), or the more in-depth coverage in Financial Metrics Pro.

By Marty Schmidt. Copyright © 2004 - Solution Matrix Limited and Marty Schmidt+. All Rights Reserved.