What is Interest?
Interest earnings and interest payments are central in modern finance. The aim is to earn more with borrowed funds than the cost of borrowing.
Having the use of money for a time span has value—a value that is real and measurable. The practical measure of this value is Interest.
Define Interest and Interest Terms
Borrowers and others who have temporary use of funds that are not their own typically pay, while lenders or investors who make their own funds available for use by others receive payment.
- The primary part of these payments for use of funds is interest.
- The amount borrowed or invested is the Principle.
- The interest payment covering a specific time period is a given percentage of the principle. The percentage figure is the Interest Rate.
Interest Rates Are Not Entirely Predictable
- Interest earnings and interest payments are central tools in the practice of modern finance, that is, making the best use of the organization's financial resources.
- Financial officers try to borrow funds and use them to earn more than the cost of borrowing.


Individual investors and businesspeople of all kinds try to do the same. The challenge for all concerned is that interest rates often change over time. And, interest rates depend on factors not entirely predictable. As a result, Interest earnings and interest costs are also not entirely predictable. Note especially that the financial mathematics in sections below are relatively straightforward, but the results they predict are "certain" only when the interest rates are "certain."
Explaining Interest Concepts in Context
This article presents the basic terms and concepts for calculating interest payments and interest earnings in the context of interest-related terms from economics, banking, and business analysis, emphasizing three themes:
- First, the definition and meaning of interest in business borrow, lending, and discounted cash flow analysis.
- Second, examples showing how interest grows with compounding and the impact of interest rate and compounding frequency.
- Third, different methods for defining and calculating interest rates for loans and investment returns.
Contents
Calculating Single Period Interest
Basic Interest Calculations
Potential borrowers, lenders, and investors have a keen interest in knowing exactly what they will pay, or earn, before taking action. Sections below show how to address these concerns by calculating interest charges and transaction costs. These calculations are relatively simple and straight forward, once a few interest parameters are defined. Remember, however, that the results are certain only when interest rates are fixed for the life of the loan or investment.
Calculating Interest and Future Value
In the case of a loan or an investment (such as an interest-paying bank deposit), interest calculations begin with an interest rate and the time span it covers, such as "8.0% per year." The analyst also needs the initial investment amount (the principal), and the number of such periods the funds will stay on deposit, such as one year or ten years. The formula in Exhibit 1 uses these data to answer the investor's question about interest earnings above.

For an investment, Future Value FV is the sum of the principal returned to the investor after the final investment period, plus all interest earnings. (Note that formulas here intentionally use the same symbols appearing in other articles on time-value-of-money concepts, such as discounted cash flow.)
Example: Calculating Single-Period Interest and Future Value
Consider a one-year $100 investment, returning interest at an annual rate of 5.0%. What is the future value (FV) of this investment after one year? How much interest does it earn? For this example:
PV = $100.00
i = 5.0% = 0.05 per year
n = 1 year
Future Value (FV)
FV = PV (1 + i )n
= $100.00 ( 1.0 + 0.05 )1
= $100.00 ( 1.05)
= $105.00
Total interest earnings = FV – PV
= $105.00 – $100.00
= $5.00
Multi-Period Future Values with Interest Compounding
Example Calculations
When interest earnings remain on deposit after one period, they add to the principle for the next period's interest calculation.
Define Compound Interest
When Interest earned in one period earns interest on itself in subsequent periods, the new earnings are compound interest.
Earning interest on interest earnings is compounding.
Each interest-earning period in which compounding occurs is a compounding period
For example, what is the FV after two years of a $100 investment, paying 5% per year interest? What is the FV after ten years, at the same interest rate?
For the two-year investment:
PV = $100.00
i = 5.0% = 0.05 per year
n = 2 years
Future Value after two years (FV2)
FV2 = PV (1 + i )2
= $100.00 ( 1.0 + 0.05 )2
= $100.00 ( 1.1025)
= $110.25
For the ten-year case, n =10 years
FV10= PV (1 + i )10
= $100.00 ( 1.0 + 0.05 )10
= $100.00 ( 1.6289)
= $162.89
Graphing Compound Interest Growth
Exhibit 2 below plots future values as a function of the number of periods. Note especially how the plot results in upward curving lines. This shape is characteristic of exponential functions such as the FV formulas above. And, the exhibit also shows that a few percentage points difference in interest rates (5% vs. 8%) lead over many periods of substantial differences in future value.
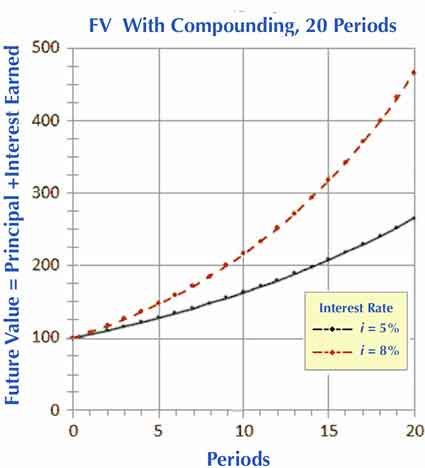
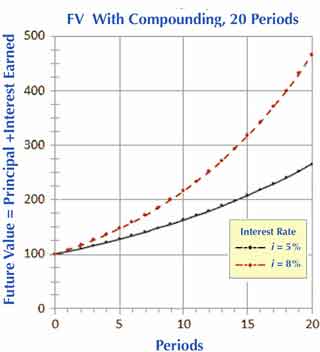
Compound Interest is Exponential Growth
Exponential Growth Defined and Explained
For those who wonder why the exponent for (1+ i ) works this way for compound interest, note that the formula FV2 = PV (1 + i )2 is mathematically equivalent to taking FV1 (the FV after one period, including the first year's interest), and making that the new PV for another interest calculation for the second year.
PV (1 + i )2= PV ( 1+ i )1 (1 + i )1
The expression on the right transforms into the expression on the left by recognizing that two identical ( 1 + i ) terms multiply by stating the term just once and adding their exponents ( 1 + 1 = 2 ). Therefore, to obtain FVs based on compound interest, when the interest rate "i" stays the same from period to period, simply set the exponent for a single ( 1 + i) term equal to the number of periods.
Note that FV growth that builds with an exponent in this way is known, not surprisingly, as exponential growth. As a result, the two upward-arcing curves in Exhibit 2 above are characteristic of exponential growth.
Does Compounding Frequency Impact Growth?
How Does Continuous Compounding Work?
What is the future value of a two-year investment when the compounding periods are one month instead of one year?
What is FV with daily compounding? And, what is FV with continuous compounding?
Interest on financial investments is often calculated, or compounded, on a semiannual, quarterly, monthly, or daily basis, as well as on an annual basis. Compounding may even occur on a "continuous" basis. The examples above use annual (1-year) compounding periods, but shorter periods mean that compounding occurs with a higher frequency.
For mufti-period loans or investments, compounding frequency also has an impact on final future value.
A ten-year $100 investment paying 5.0% for each annual period, leads to the FV of $162.89 after ten years, as the example above shows.
A ten-year $100 investment with monthly interest compounding, at a monthly rate one-twelfth the annual 5% (0.4167% per month), leads to an FV of $164.70 after 120 months (10 years).
Nominal Interest Rates for Different Compounding Frequencies
When comparing loans or investments with different compounding frequencies, it is helpful to have an annual rate of some kind for each to facilitate comparison. The following sections define and illustrate several approaches for quoting this yearly rate.
However, note that examples in this section refer to an annual rate usually called simply the nominal interest rate. Analysts define nominal rate as follows:
Nominal interest rate = ( Interest rate per period ) ( Number of periods per year )
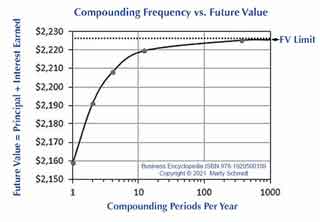
When calculating interest with monthly compounding periods at, say, 1.0% per period, the nominal interest rate is 12.0%. That is, 12 x 1.0% =12.0%. Exhibit 3 below shows how the Future Value formula from Exhibit 1 changes slightly to accommodate different compounding periods.


Future Values vs. Compounding Frequency
Example Calculations
Consider a 10-year interest-paying bank deposit of $1,000, where the nominal (annual) interest rate is 8.0%, with monthly compounding. Using the symbols above for this case:
PV = $1,000.00
i = 8.0% nominal interest rate per year
q = 12 compounding periods per year
Y = 10 years of compounding
FV = PV ( 1 + i / q )Yq
= $1,000 ( 1.0 + 0.08 / 12 )(10)(12)
= $1,000 (1.00667)120
= $1,000 (2.21964)
= $2,219.64
For the same deposit with continuous compounding:
PV = $1,000.00
i = 8.0% nominal interest rate per year
Y = 10 years of compounding
e
= 2.71828182845904... (e is a constant and always has this value)
FV = PV eYi
= ($1,000) e(10)(0.08)
= ($1,000) e0.8
= $2,225.54
Note that expressions involving the natural logarithm constant e calculate easily in Microsoft Excel with the EXP function. The Excel version of the last FV formula is:
= 1000*EXP(10*0.08)
Example Results:
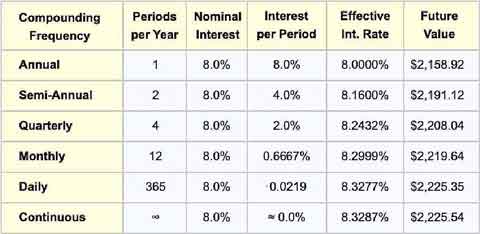
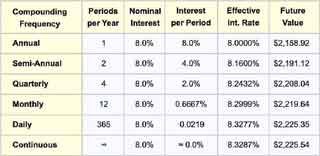
FV For Different Compounding Frequencies
Table 1 compares FV results, for example, $1,000, ten-year deposit using a nominal 8.0% interest rate with different compounding frequencies:
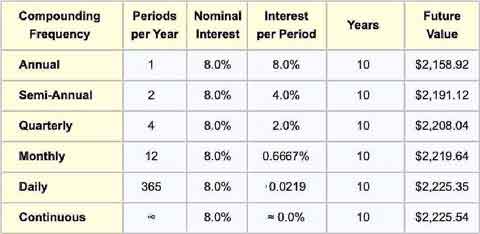
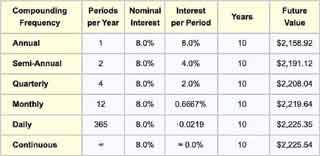
The table shows clearly that FV increases as compounding frequency increases, approaching its maximum limit when the frequency is infinite (continuous compounding). Note also that the relationship between compounding frequency and future value is natural to grasp when the connection appears in a graph, as Exhibit 4 shows.

Rates for Comparing Loans and Investments
Define Your Terms!
Examples above refer to a nominal interest rate. That is one basis for comparing interest costs and interest returns from different compounding plans. There are other interest rate methods in common usage, however, for approximately the same purpose.
Unfortunately, some of these rate methods have several names, and one (annual percentage rate, or APR) not only has several names but has different definitions in different countries. As a result, the distinctions among different rate terms can seem obscure or confusing.
To avoid confusion in the following discussion, keep in mind that all these interest terms fall essentially into just three classes, "Nominal," "Effective," and "Real."
Nominal Interest Rates and Nominal Rate Terms
Define Your Terms!
Four similar terms referring to nominal interest rates have the same meaning:
Nominal Interest Rate
Nominal Annual Rate
Annual Percentage Rate Nominal
APR Nominal Rate
Nominal interest rate by any of these names has the same definition:
Define Nominal Interest Rate
Nominal Interest Rate (percentage) describes loan or investment interest on an annual basis. The nominal interest rate is …
- Not adjusted to reflect any of the following: inflation, the contributions of compounding, or other investing or borrowing costs
- A term used primarily when the compounding frequency (e.g., 12 times per year) does not equal the unit of time span for describing the rate (e.g., "8% per year").
Calculating Nominal Interest Rate
The following formula shows how to calculate a nominal interest rate.
Nominal interest rate = ( Interest rate per period ) ( Number of periods per year )
Example: When interest builds with monthly compounding periods at 1.0% per period, the nominal interest rate is 12.0%. That is, 12 x 1.0% = 12.0%
Nominal interest rates provide a quick and easy-to-understand way to compare loans or investments with different compounding frequencies. The term "nominal" applies because they are not adjusted to reflect inflation, compounding, or other costs (as are the rates below).
Effective Interest Rates and Effective Rate Terms
Define Your Terms!
Five similar-sounding terms referring to nominal interest rates have the same meaning:
Effective interest Rate
Annual Equivalent Rate AER
Annual Effective Rate AER
Effective Annual Yield
Annual Percentage Rate APR
These five terms are equivalent, except for some slight usage differences. All provide investors with a means of addressing questions such as this:
Would an investor prefer to receive interest from daily compounding or annual compounding?
The investor can answer the question by finding the effective interest rate for both the daily and annual compounding periods. Note for example:
- With yearly compounding, a ten-year deposit of $1,000 earning interest at a nominal rate of 8%, leads to a future value of $2,159.
- The same deposit at an 8% nominal rate leads to a future value of $2,225 with daily compounding.
Both scenarios use the same principal, same deposit time, and same nominal rate, but the daily compounding effectively returns more. Interest rate methods with the name w "effective" attempt to recognize the contribution of compounding frequency. The purpose is to facilitate borrowing plan comparisons.
Calculating Effective Interest Rates
Example Calculations
The "effective interest rate" concept takes into account the impact of compounding frequency. The first formula gives the effective interest rate "r" for a loan or investment in Exhibit 5 below.

Example: Finding Effective Interest Rates for Different Compounding Periods
Effective interest rate calculation examples: For a $1000 deposit at a nominal interest rate of 8.0% ( i = 8.0%), compounded annually ( n = 1 ), the effective interest rate is the same as the nominal rate:
r = ( 1 + i / n ) n– 1
= (1 + 0.08)1
– 1
= 0.08 = 8.0%
However, the same investment at the same 8% nominal interest rate, leads to a different effective rate with daily compounding ( n = 365):
r = ( 1 + i / n ) n– 1
= (1 + 0.08 / 365)365
– 1
= ( 1.00021917808)365
– 1
= 1.08327757178281 – 1 = 0.0832775718
= about 8.33%
These results say that an investment of $1,000, with a nominal interest rate of 8.33% and annual compounding, has a future value equal to a $1,000 investment with a nominal rate of 8.00% compounded daily. With daily compounding, in other words, the effective annual rate is 8.3277%%.
Example:
Finding Effective Rate with Continuous Compounding
The maximum effective interest rate occurs under continuous compounding. For an investment with continuous compounding, at the same 8% nominal interest rate, the effective rate is:
r = ei
– 1
= (2.7182828…)0.08
– 1
= 1.083287068... – 1.0 = 0.083287068
= 8.3287068%
= about 8.3287%
Clearly, the differences in effective interest rates between the daily compounding situation ( n = 365) and continuous compounding are small—about one one-thousandth of one percent.
Effective and Nominal interest Rates
vs. Compounding Frequency
Table 2, below parallels Table 1 above, showing different compounding frequencies for a deposit with an 8.0% nominal interest rate. However, Table 2 shows how effective interest rate changes with compounding frequency:
Analysts and investors use several different terms for Effective interest, as it appears above. They sometimes call effective interest rate the following: Annual effective rate (AER), and Annual equivalent rate (also AER). And, when this percentage applies to an interest-paying investment, such as a bank certificate of deposit (CD), they may use the terms Annual effective yield or Effective annual yield for the same calculation. This usage of "yield" should not be confused with the different calculation used in evaluating bond investments, also called Yield or Yield to maturity.
For more on these terms in the context of bond investments, see the encyclopedia entry bond.
Disclosing Annual Percentage Rates
It's the Law!
The effective Interest rate is also at the center of the interest rate term Annual percentage rate, or APR. Annual percentage rate—as the term appears in most countries—often has a legal definition from the government, meant to provide depositors or investors with an accurate measure for comparing returns from different potential investments.
APR definitions usually include the effective interest rate, but also reflect some borrowing costs that other than "interest" such as loan origination fees, periodic maintenance fees, and others. See the entry cost of borrowing for more on the role of borrowing costs besides interest.
Disclosure Rules Differ from Country to Country
In the United States, the calculation and disclosure of APR are governed by the Truth in Lending Act (TILA) of 1968 (a federal law). In the US, the TILA specifies APR as the nominal interest rate, but with adjustments to include specific non-interest costs.
The US TILA does not attempt to regulate rates and costs that lenders may charge, but instead, addresses disclosure. For mortgages, for instance, the TILA prescribes that lenders must disclose the APR to applicants within days of applying.
APR is defined in the United Kingdom by the Consumer Credit Act of 1974. This law requires that lenders publish the APR and make it prominently visible for all regulated loans.
The European Union has issued a series of directives over time (e.g., 87/102/CEE and 98/7/EC) requiring member states to move closer to uniformity on the components and calculation of APR, while still allowing some differences between countries. The primary purpose of these directives is to regulate disclosure.
Lenders In Canada must disclose APR (also called Effective interest rate, EIR) for loans, mortgages, and credit card debt. And, lenders must use a calculation that factors in borrowing costs including loan origination fees, account maintenance fees, others.
The Australian Consumer Credit Code (ACCC) of 2003 requires that lenders state APR for all consumer loans and credit, using a formula that recognizes interest as well as fees (upfront fees, ongoing fees, and exit fees). Lenders in Australia call this rate the AAPR (Average annual percentage rate).
Defining Real Interest Rate
Define Your Terms!
Lenders sometimes use the real interest rate concept to adjust stated interest rates for loans or investments to compensate for the effect of inflation. Most define real interest rate just as the nominal interest rate for a loan or investment minus the inflation rate:
Real interest rate = Nominal Interest Rate – Inflation rate
When inflation is running at an annual rate of, say, 2.0% for an economy, a loan or investment with a nominal interest rate of 8.0% has a real interest rate of about 6.0%. With real interest rates, however, remember (1) that inflation rates can and usually do change somewhat from year to year, and (2) inflation rates differ substantially from country to country.
When the inflation rate is high, interest payments and interest charges tend to be higher. And, when the inflation rate is low, interest rates are also low. The result is that real interest rates exhibit more stability in changing economies than do the nominal interest rates.
Analysts can determine real interest rates for evaluating historical loans and investments and past inflation rates with high confidence. Looking forward in time, however, to assess potential real interest rates from investments, future inflation rates are necessarily more uncertain.

