What is Internal Rate of Return IRR?
Interpreting IRR in a way that makes practical sense for investors and decision-makers is a challenge.
Internal Rate of Return(IRR) is a financial metric for cash flow analysis, popular for evaluating the performance of investments, capital acquisitions, project proposals, programs, and business case scenarios. Like other cash flow metrics—NPV, Payback period, and ROI—the IRR metric takes an "investment view" of financial results and addresses questions like these:
- Does the investment have an acceptable rate of return?
- Will the investment lead to a net-gain or a net loss?
- How does one investment option compare to other available options?
"Investment view" means that each metric addresses such questions by comparing the magnitudes and timing of cash flow returns to cash flow costs, while each makes the comparison in a unique way. As a result, each carries a different message about the value of the action.
Define Internal Rate of Return IRR
The internal rate of return (IRR) for a cash flow stream is the interest rate (discount rate) that produces a net present value of 0 for the stream.
Sections below explain what a discount rate that leads to a 0 NPV says about investment returns and costs. Not surprisingly, interpreting IRR results in a way that makes practical sense for investors and decision-makers is a challenge.


IRR is All About a Cash Flow Stream
IRR analysis begins with a cash flow stream, a series of net cash flow results expected from the investment (or action, acquisition, or business case scenario). Consequently, cash flows for IRR analysis might look like the figure below. Note especially in the chart:
- Each bar represents the net of cash inflows and outflows for one two-month period.
- Positive values are net inflows, and negative values are net outflows.
The complete set of net cash flow events is a "cash flow stream," which might appear in graphical form as Figure 1.
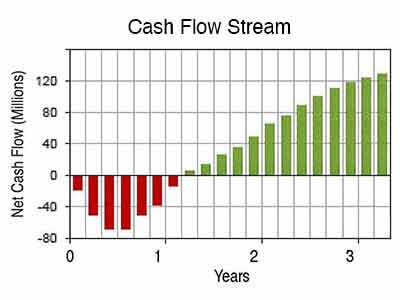

Notice especially the shape, or profile of this example stream. This figure represents a typical investment curve because:
- Net cash outflows at the outset and net cash inflows in later periods mean that costs initially exceed incoming returns.
- Returns eventually outweigh the costs and the investment brings a net gain.
The IRR metric "expects" this kind of cash flow profile—costs first and benefits later. As a result, when the cash flow stream has this profile, an interpretable IRR probably exists. When cash flow events have another profile, instead, the stream may not have an IRR. Also, other strange IRR results may also appear when the profile is something other than an investment curve. As a result, other profiles can lead to more than one IRR for the same stream or a negative IRR for the stream. Consequently, in such cases, the resulting IRRs are either very difficult to interpret or meaningless
Internal Rate of Return: Many Use IRR, Few Understand IRR
Most people in business have at least heard of the "internal rate of return." The name is familiar because financial officers often require an IRR estimate to support budget requests or action proposals. IRR is a favorite metric of many CFOs, Controllers, and other financial specialists.
Also, some businesspeople know of IRR because many organizations define a hurdle rate as an IRR. They specify, that is, an IRR rate that incoming proposals must reach or exceed to qualify for approval and funding.
Two possible reasons for IRR's popularity may be the following:
- First, many in the financial community see IRR as more "objective" than the net present value (NPV). They have this view because NPV results from arbitrarily chosen discount rates while IRR, by contrast, results entirely from the cash flow figures themselves and their timing.
- Secondly, some also believe that IRR readily compares return rates with inflation, current interest rates, and financial investment alternatives. Note especially in the discussions below that this belief is sometimes supportable and sometimes not.
It should be no surprise to learn that most businesspeople who are not in finance have a limited or poor understanding of IRR and its meaning. It may be more surprising, however, to learn that research on professional competencies often finds that most financial specialists who require IRRs with proposals or funding requests are themselves mostly unaware of IRR's serious deficiencies. Many are also unable to explain its meaning and proper use.
Emphasize IRR Meaning and Interpretation
This article further explains and illustrates internal rate of return in context with related terms and concepts, emphasizing four themes:
- Firstly, IRR meaning and interpretation.
- Secondly, common misconceptions and misuses of IRR.
- Thirdly, comparing IRR to other financial metrics for cash flow analysis, including NPV, ROI, and Payback Period.
- Fourthly, presenting modified internal rate of return (MIRR) as an easy-to-understand alternative to IRR.
Contents
Defining Internal Rate of Return IRR
First Textbook Definition Illustrated Example


As the word "return" in its name implies, an IRR view of the cash flow stream is an investment view. "Investment view" means essentially that the metric compares outgoing funds to the magnitude and timing of incoming returns.
The best-known IRR definition explains this comparison in terms that call for a basic understanding of cash flow discounting concepts: present value, "net present value" (NPV), and the role of the discount rate (interest rate) in determining NPV.
fIRR Definition 1 (Textbook Definition):
The internal rate of return (IRR) for a cash flow stream is the interest rate (discount rate) that produces a net present value of 0 for the stream.
For most businesspeople, however, that definition is less than satisfying when they first see it. As a result, many businesspeople ask: What does that tell me about returns and costs?
The First Interpretation of IRR Meaning: IRR As a Measure of Risk
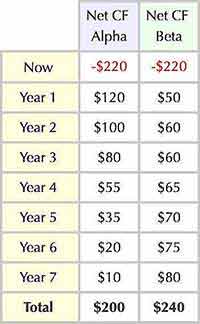

Consider two investment proposals competing for funding: Case Alpha and Case Beta. Table 1 shows the net cash flow streams forecasts for Alpha and Beta investments.
Different IRRs for Front Loaded and Back Loaded Cash Flow Streams
Both cases call for an initial cash outlay of $220. However, Case Alpha brings a net gain of $200 over seven years while case Beta brings a net profit of $240 over the same seven years. For that reason, it is tempting to designate Alpha as the better business decision, because Alpha ultimately returns greater net CF. Before deciding, however, experienced analysts will also want to compare these CF streams on the basis of IRR and possibly other metrics, as well.
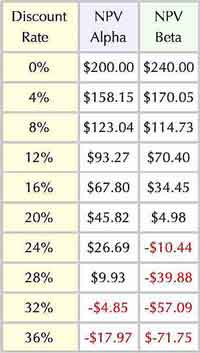
Before finding IRRs and other metrics, note especially from a graphical display (Figure 2) how the two cash flow streams differ.
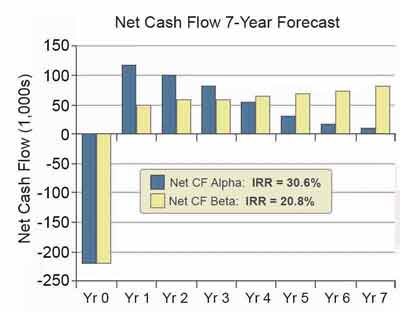
Both cash flow streams qualify as investment curves but one is front-heavy (Alpha) while the other (Beta) is back-heavy.
- Case Alpha (dark blue bars) has substantial early returns, but these diminish year by year. Case Alpha is, therefore, front-loaded. Alpha's profile could represent the acquisition of an income-producing asset that becomes less productive or more costly to maintain each year.
- Case Beta (yellow bars) has smaller returns at first, but Beta's returns grow each year. Beta is therefore back-loaded. Beta's profile could result from funding a product launch that returns greater profits each year.
Here, the analyst is comparing two different kinds of investments with the same metric, IRR, to help decide which is the better business decision. IRR results from a spreadsheet or other software analyses of the figures are as follows:
Case Alpha: IRRA = 30.6%
Case Beta: IRRB = 20.8%
IRR is the Discount Rate That Brings NPV to Zero


Table 2 and Figure 3 show the result of applying IRR Definition 1, that is, finding IRR as the discount rate that brings an NPV of 0. Note that this example shows only one of the above cash flow streams from Table 1, Case Alpha.
In Figure 3 below,
- Dark blue bars are future value net cash flows for Case Alpha.
- Gray bars are present values of the same cash flows at IRR discount rate of 30.6%.
You should be able to see or imagine that the heights of the seven positive (upward pointing) gray bars starting with Yr 1 add up precisely to the length of the one negative (downward pointing) light gray bar at "Now." As a result, the IRR definition is satisfied because the total of positive PVs equals the sum of negative PVs.


First IRR Interpretation
IRR As a Measure of Risk
Which investment choice should the analyst recommend, Case Alpha or Case Beta? Alpha has an IRR of 30.6%, while Beta has an IRR of 20.8%. Using IRR as the decision criterion—and with other factors being equal—the analyst will recommend the case with the higher IRR (Alpha) as a better choice.
Analysts make this recommendation because a high IRR indicates low risk. That is, IRR shows just how high inflation rates or risk probabilities have to rise to eliminate the present value of this investment.
- For Case Alpha, the discount rate has to reach 30.6% to drain Alpha's results of present value.
- Case Beta loses all present value if the discount rate rises to 20.8%.
Most people, however, find this first interpretation of IRR of limited value for evaluating and comparing investment proposals. Later sections below, therefore …
- Explain in more depth the IRR definition in terms of incoming and outgoing cash flows.
- Compare IRR results with other cash flow metrics.
- Present another cash flow metric that is easier to interpret than IRR. This metric is the modified internal rate of return (MIRR).
Finding Internal Rate of Return IRR
Can You Calculate IRR?
Analysts calculate cash flow metrics such as NPV, ROI, and even payback period, directly from formulas. However, the verbal IRR Definition 1 above does not readily lend itself to expression as a formula.
Remember first that IRR Definition 1 refers to another metric that does calculate from a formula, net present value NPV. Figure 4 below shows the method for calculating NPV for a cash flow stream using end-of-period discounting.

Here, the FVs are net cash flow figures for each period, i is the discount rate, while n is the number of periods. For Case Alpha and Case Beta, n = 7. That is, the cash flow stream covers seven periods and each period is one year.
Consequently, when met with a request for an "IRR formula," about the only response possible is to start with (1) the NPV formula above and (2) the FVs (net cash flow values), and then proceed as follows:
To Find IRR
- Set NPV equal to 0.
- Solve the formula for i.
- IRR = i when NPV = 0.
In reality, there is no easy analytic solution to this request, and most people will be unable to solve the NPV = 0 equation for i. As a result, It is more accurate to say that analysts do not calculate IRR. Instead, they find IRR by indirect methods. In practice, analysts instead find IRR either by (1) graphical analysis or (2) as spreadsheets do, through a series of approximation trials (successive approximations).
Finding IRR With a Graphical Solution
Businesspeople needing to find an IRR for a cash flow stream rely almost always rely on software for a numerical result, that is, on computers or electronic calculators. Before the computer era, however, the graphical solution was overwhelmingly the method of choice. The only alternative at that time, was the very labor-intensive method of successive approximations, which called for a long series of tedious hand-calculations on paper.
Nevertheless, the graphical solution for IRR is helpful, now, for understanding or explaining the IRR definition IRR definition:
The internal rate of return for a cash flow stream is the interest (discount) rate that produces a net present value of 0 for the stream.

The graphical IRR is an easily-to-understand picture of the relationship between NPV and discount rates. It is thus a learning aid for teachers, but also useful decision-support tool for those deciding exactly which interest levels to designate as financial hurdle rates.
Example IRR Graphical Solution
The graphical approach begins with a table of discount rates and NPV values, such as Table 3. This example shows NPVs for Alpha and Beta cash flow streams at ten different discount rates. Note especially that NPVs here derive from the original net cash flow figures and the NPV formula above. To produce this table, the analyst had to calculate 20 NPV figures.
The data above are plotted below, showing the relationship between discount rate (horizontal axis) and resulting NPV (vertical axis).
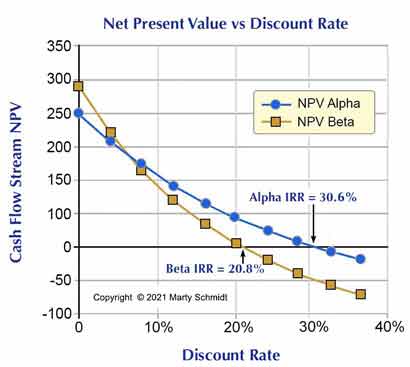
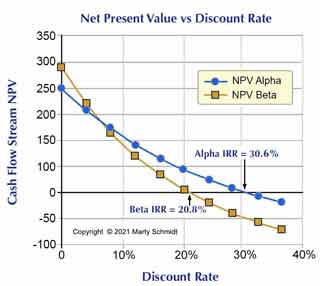
The chart shows that increasing the discount rate lowers NPV for both streams. The graph also shows how cash flow streams with a positive total net cash flow can produce NPVs that are either positive or negative, depending on the discount rate.
Regarding IRR, note especially that Alpha's NPV reaches 0 at a discount rate of 30.6%, while Beta's NPV reaches 0 at a discount rate of 20.8%. From the graph, therefore, the analyst concludes that IRRA = 30.6%. and IRRB = 20.8%.
Finding IRR With a Spreadsheet Solution
The NPV curves above are useful for helping show precisely the meaning of IRR Definition 1. Today, however, most people in business use spreadsheets or pre-programmed calculators to find IRRs.
Either way, a program starts the approximation process by choosing a discount rate to calculate NPV for a cash flow stream. If the resulting NPV is not 0, the program adjusts the discount rate, repeats the NPV calculation, and checks again to see if NPV = 0. Trials of this kind repeat hundreds or thousands of times until a discount rate that does produce NPV = 0 appears. In Microsoft Excel, for instance, these trials continue until Excel finds an IRR accurate to 0.00001 percent. Because trials execute very quickly, however, the IRR result seems to appear immediately with data entry.
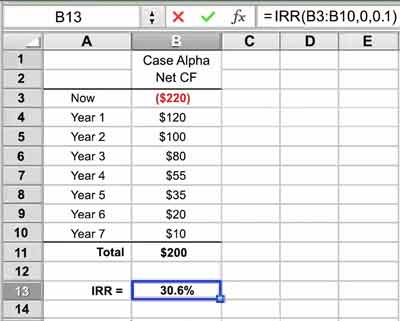

The analyst, for example, might enter a Microsoft Excel IRR function into an Excel formula like this:
= IRR (B3:B10, 0.1)
The spreadsheet cell with this formula shows the IRR for a worksheet range with net cash flow figures in cells B3 through B10. These cells could, for instance, hold the eight cash flow values for Case Alpha in the example above. Note also that the 0.1 figure is simply a user-provided first guess at the IRR. The guess is just a starting discount rate for calculating NPV on the first iteration, and it can be almost anything.
The IRR value itself appears in the cell holding the above Excel formula. Here, the actual numerical result in cell B13 is 0.306325. The analyst will probably format cell B13 as a percentage so that the IRR result looks like this: 30.6%
Re-Stating the IRR Definition
Why Is it Called Internal Rate of Return?
The textbook IRR Definition above explains how to find an IRR but says very little about what it represents. As a result, IRR's more basic meaning is usually easier to understand by restating the IRR definition in a way that refers to investment financing costs and reinvested returns.
IRR Definition Restated:
The Internal Rate of Return (IRR) For a Cash Flow Stream Relies on Two Assumptions:
- There is a financing cost (or opportunity cost) for using the invested funds. The calculation assumes that invested funds incur financing costs (or opportunity costs) until the final cash flow event.
- Incoming returns are re-invested for the time remaining until the last cash flow event.
IRR Definition 2
"IRR is the single interest rate for financing costs and for reinvestment earnings that sets the total gains precisely equal total costs."
Table below shows how IRR achieves this balance:
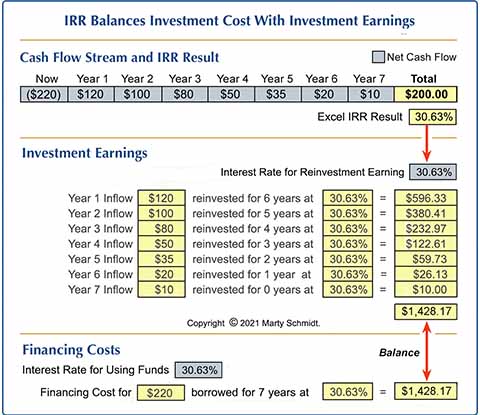
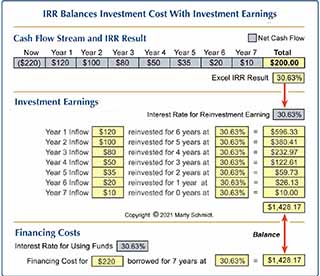
This example shows how the IRR rate causes total investment returns (cash inflows) to equal total investment costs (cash outflows). First, the spreadsheet finds IRR for the cash flow stream (blue cells). This rate then serves to calculate both returns and investment costs. Using the IRR rate, "Total from inflows reinvested" equals "Financing costs."
At IRR, Investment Costs Balance Investment Returns
In the example, a cash outflow of $220 (at "Now") represents initial investment costs. Subsequently, each year after that, the investment brings positive cash flow returns. Excel's IRR function result appears in the yellow cell below Year 7 net cash flow, reporting an IRR of 30.63% for the net cash flow stream running from "Now" through Year 7. Therefore, the example uses the same IRR value of 30.63% for calculating both (1) reinvestment earnings and (2) financing costs.
- Consider first the interest earned by re-investing the incoming cash flows from Years 1 through 7. Because each incoming return is re-invested for the remaining years at an annual interest rate of 30.63%, the total seven-year gains are $1,428.17 (inflows + interest earned).
- Now, assume the initial cash outflow of $220 is borrowed and financed at the same 30.63% annual rate. Because the total cost of repaying this loan is also $1,428.17, exactly (initial cash outflow plus financing), the IRR rate exactly balances total costs with total gains.
Interpreting the Second IRR Definition
Financing Costs and Reinvestment Gains
The second definition example above should suggest a reason that financial people often trust IRR as an essential decision criterion.
- First; remember that the IRR result assumes the use of funds to pay investment costs brings additional costs, either borrowing costs or opportunity costs.
- Second, remember that incoming returns are reinvested, earning additional gains.
These two assumptions provide meaning for another IRR interpretation, namely that the analyst will compare the IRR rate to actual financing rates and real rates for reinvesting. These comparisons must be interpreted carefully, however, because It is easy to over-interpret or misinterpret IRR at this point.
Tempting But Faulty IRR Reasoning
When an investment proposal produces IRRs like those shown above—30.6% for example—some people reason as follows:
"For this investment, we will not really borrow or pay an opportunity cost at the IRR rate. Therefore, our real financing cost will be subject to a much lower interest rate, closer to our cost of capital, probably less than 10%. Thus, [the reasoning goes], the investment is a net gain because financing rates will certainly be under 10%, while returns represent earnings at a much higher rate, something like 30.6%."
In reality, that conclusion may or not be supportable, depending on the real financing rates (or opportunity costs) and the real reinvestment rates that apply. The reasoning is arguably valid only when the IRR rate is close to the real "cost of capital" and actual reinvesting rate. When IRR is substantially different from actual rates, however, the same conclusion is more likely misleading or entirely wrong.
Why Does IRR Sometimes Overstate the Value of Returns?
This kind of reasoning can grossly overstate the value of actions like Case Alpha. Suppose, for example, that the real earnings rate from reinvesting returns is close to 8%, much lower than the stream's IRR of 30.6%. Notice especially:
- Cash flow stream Alpha has its most substantial gains in the first and second years of the 7-year analysis period. That is, Case Alpha is "front-heavy," or "biased" towards the early years. IRR, therefore, overstates the real earnings rate because it assumes year-1 and year-2 gains will earn at a 30.6% rate for all the remaining years. In fact, this long term of high-rate earnings will be absent.
- Cash flow stream Beta, on the other hand, has a lower IRR than Alpha, but when the analyst compares real return earning rates to the earnings that IRR assumes, Beta has fewer "missing" gains of this kind than Alpha.
- IRR thus overstates the real value of Case Alpha far more than it does for Case Beta for two reasons:
- First, stream Alpha is front-heavy while stream Beta is back-heavy.
- Second, Alpha's IRR is further from the real reinvestment rate than Beta's IRR.
In conclusion, one can reasonably view the investment outcome as a net gain when IRR exceeds the organization's cost of capital. Beyond this, however, further assessment of IRR magnitude can be problematic, especially when:
- IRR dramatically exceeds "cost of capital" and the real earnings rate for returns.
- Comparing two cash flow streams with different profiles as in the example above. This point appears again in the discussion below on Lease vs. Buy comparisons.
Modified Internal Rate of Return MIRR
Is MIRR Better Than IRR? MIRR is Easier to Interpret.
The meaning of IRR magnitude is difficult to interpret, as shown because IRR can differ from the actual financing and earnings rate for returns. It is natural to ask, therefore, "Why not use a different metric instead of IRR, that does reflect the real financing cost rate and real earnings rate for returns?"
In fact, precisely this solution is readily available as the modified internal rate of return (MIRR) metric.
Example: MIRR Calculates Directly From a Formula
Input data for MIRR include the same net cash flow figures as IRR, but the MIRR calculation also requires as input a financing rate and a reinvestment rate. Here for comparison are the IRR and MIRR results for Cases Alpha and Beta from above. MIRR for this example assumes an 8% earnings rate for reinvested returns and a 6% financing rate on costs.
Case Alpha:
IRRA = 30.6% MIRRA = 15.1%
Case Beta:
IRRB = 20.8% MIRRB = 14.7%
Notice immediately that Case Alpha also has a higher MIRR value than Case Beta, but both MIRR values are much closer to each other than are the two IRR values.
The interpretation of MIRR is easier to understand after showing first how to calculate MIRR. Unlike IRR, MIRR derives directly from a formula:


To obtain MIRR, the analyst finds:
- Future values of cash inflows using the reinvestment rate.
- Present values of the cash outflows using the financing rate.
The radical sign calls for the nth root of the (Future Value)/(Present Value) ratio. The number of periods, in this case, n, is 7. The MIRR value is the root, less 1.0.
MIRR Example Calculation
For example, cash flow stream A using a reinvestment rate of 8%:
FV (Positive Cash Flows)
= $120·(1.08)6+ $100·(1.08)5+ $80·(1.08)4
+ $55·(1.08)3 +...+ 35·(1·08)2+ $20·(1.08)1 + 10·(1.08)0
= $190.42 + $146.93 + $108.84 + $69.28
+ $40.82 + $21.60 + $10.00
= $587.91
The analyst also calculates "Net Present Value" of the negative cash flows, applying the financing rate (given as 6% in this case). Note, however, that for this simple example there is only one negative cash flow ($220) and because that occurs immediately ("Now"), its present value shows 0 discounting effects.
PV (Negative Cash Flows)
= ($220)·(1.06)0 = ($220.00)
Negative cash outflows will have negative "present values," so the formula precedes the Present Value sum with a minus sign ("–") making it a positive number. Using the above formula, MIRR for Investment Case Alpha is thus:


MIRR Meaning is Easy to Understand
Here, at last, is an investment result with a clear, easily understood meaning.
- If the original $220 cost merely is put on deposit in the bank, earning interest at the MIRR annual rate of 15.1% for seven years, the total investment value with compound interest will be $587.91.
- If instead the investment cost of $220 is paid, and the investor reinvests the projected cash inflows from Case Alpha at 8.0%, the total investment value for them with compound interest earnings will be the same $587.91.
- Similarly, Case Beta has a MIRR of 14.7%. If Case Beta's initial cash outflow merely is put on deposit for seven years, earning interest compounded at the MIRR rate, the total value will be 573.76.
- If instead, the investor reinvests the projected incoming cash flows from Case Beta at the rate of 8.0%, the total value after seven years will be the same $573.76.
Note: To check these calculations yourself, use the more precise MIRRA rate of 15.0757% and MIRRB rate of 14.6732%.
In simpler terms, taking the actions proposed in Case Alpha and Case Beta brings the same results as merely putting the initial costs in the bank and receiving compound interest earnings at the MIRR rate!
Notice that IRR results show a significant advantage for Alpha over Beta. The relative position of Alpha over Beta is much smaller in the MIRR results. In conclusion, most people can easily compare MIRR results with compound interest growth and understand the magnitude of the MIRR differences. Understanding the meaning of the IRR difference is more problematic
Finding MIRR with Excel
Incidentally, the MIRR formula is, in fact, a geometric mean. The same formula is used to find cumulative average growth rate for figures that grow exponentially such as compound interest earnings. And, calculations like those above can be avoided entirely by simply using Excel's MIRR function. For Case Alpha, whose cash flows are located in cells B3 through B10, using a reinvestment rate of 8% and financing rate of 6%,
Excel's MIRR function for this example would be:
=MIRR(B3:B10, 0.06, 0.08)
How Does IRR Compare to Other Cash Flow Metrics?
IRR Results vs. NPV, ROI, Payback, and Other Metrics
Examples above pose the kind of question that often confronts analysts:
Which is the better business decision, Case Alpha or Case Beta?
Financial specialists in many organizations use IRR to address such questions while also recognizing that complex decisions deserve more than a single financial metric. The prudent financial specialist, investor, or business analyst will compare both proposed actions with several financial measures. Examples below show how different "metrics" may suggest different answers to the question.
This section compares Alpha and Beta cases using (1) net cash flow, (2) internal rate of return, (3) modified internal rate of return, (4) net present value, (5) return on investment, and (5) payback period.
IRR vs. Net Cash Flow, MIRR, NPV, ROI, and Payback
IRR results in the above examples required only the net cash flow figures for each period (year).To compare investments with a broader range of cash flow metrics, however, the analyst needs access to cash flow data such as Alpha and Beta data in Table 4, below, To data on cash inflows and outflows for each period, along with the net figures.
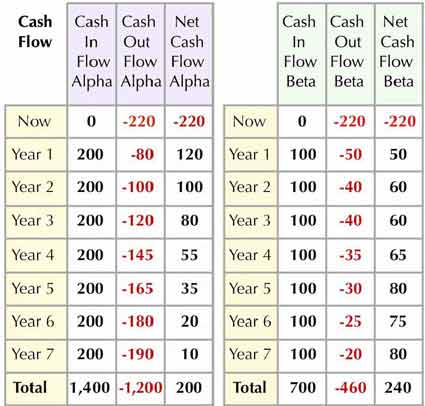

Total Net Cash Flow
The net cash flow metric favors investment Beta over investment Alpha: Alpha brings a $200 net gain over seven years, while Beta brings in $240. Beta thus has a $40 (20%) advantage in net cash flow over A. For business situations where cash flow and working capital are in short supply, that problem could mean a significant advantage for Beta. However, see the discussion on Payback Period, below, for a different view of these cash flow consequences.
Internal Rate of Return (IRR)
Case Alpha outscores Case Beta on the IRR metric, 30.6% to 20.8%. Case Alpha outscores Case Beta on the IRR metric, 30.6% to 20.8%. Both IRR figures are very likely above the company's cost of capital, and the firm no doubt sees both proposals as net gains. Some analysts will interpret Alpha's larger IRR as a signal that Alpha provides a better rate of return than Beta (assuming reinvestment of incoming cash flows). Beyond that, however, the IRR figures themselves do not show the magnitude of Alpha's real rate of return advantage over Beta.
When IRR rates exceed "cost of capital" by several times or more, the real rate of return difference between two investments depends heavily on:
- The timing of cash flows
- The cash flow stream profiles
- The actual rates available for the "cost of capital" and earnings on returns
The IRR figures say nothing about these factors.
Modified Internal Rate of Return (MIRR)
With an 8% real earnings rate for returns, Case Alpha slightly outscores Case Beta on the MIRR metric, 15.1% to 14.7%. MIRR's meaning is easily understood: MIRR essentially compares results to the growth of mpound interest earnings. Assuming that investors reinvest incoming returns at 8%, Alpha, for instance, gives the investor precisely the same result as putting the initial cash outflow on deposit for seven years and receiving compound interest earnings at the MIRR annual rate, 15.1%.
Net Present Value (NPV)
According to the net present value metric, the better investment choice ( Alpha or Beta) depends on the discount rate.
- Thus, with a 5% discount rate, Beta's NPV of $155 exceeds Alpha's $149 NPV. However, NPV leadership reverses at higher discount rates.
- With discounting at 10%, Alpha's NPV of $107 is higher than Beta's $91.
As the discount rate rises, Beta's substantial returns in later years suffer greater discounting impact than Alpha's more significant gains in the early years. This example shows one reason some financial specialists prefer IRR to NPV when choosing between competing proposals:
- The analyst arbitrarily chooses a discount rate to calculate NPV, and that choice may determine the results of the comparison as the NPV example here shows.
- IRR, on the other hand, is sometimes seen as more "objective" because it does not rely on an arbitrarily chosen rate. IRR instead uses net cash flow figures themselves to find an Interest rate that satisfies its definition.
Return on Investment (ROI)
According to the ROI metric, it is "no contest!" Beta's ROI of 52.2% beats Alpha's ROI of 18.7%, hands down. The ROI metric shown here is Simple ROI (the ratio of incremental gains to investment costs).
All cash flow metrics above show both actions as resulting in net gains for the investor. ROI alone, however, is sensitive to the magnitudes of individual annual inflows and annual outflows. By contrast, the other metrics derive only from the net cash flow figures.
Alpha's more substantial total costs ($1,200) are compared directly to Alpha's incremental gain of $200. Beta scores much higher on ROI because Beta has a more substantial increase ($240) and a much smaller total cost ($460). Other metrics that derive from net cash flow are blind to the significant differences in "costs." Alpha's higher "costs" could be problematic because the investor must budget these costs and pay them, no matter how large the returns. The investor may have trouble paying Alpha's more substantial funding costs.
Payback Period
The payback period metric shows that investment Alpha "pays for itself" in 2.0 years, while Beta needs 3.4 years to cover investment costs fully. Investors prefer shorter payback periods over longer payback for at least two reasons.
- First, the investment funds are available again for re-use sooner with a shorter payback period.
- Second, investors see the more extended payback period as riskier.
Financial Metrics Conclusions
When stating a decision criterion as a general rule, business analysts and finance officers often borrow a phrase that is a favorite of economists:
Other things being equal, the investment (or action, or decision, or scenario) with the higher IRR is the preferred business decision.
The different financial metrics comparisons above show that IRR is blind to many "other things" that may differentiate competing investments, and these things may have significant economic consequences. And, they are very rarely genuinely equal.
When the investor can or will make only one of the two proposed investments, the choice of one over the other represents so-called constrained financing. Consequently, analysts usually recommend not using IRR as a decision criterion when comparing mutually exclusive investments or actions.
Rewards Must Compare Favorably to Risks
Finally, in business investing—as in gambling—a wise investment (or a good gambling bet) is one where potential rewards compare favorably with investment risks. None of the metrics above fully measures investment risk, although risk considerations are partially visible in IRR, NPV, and payback period:
- Analysts view an investment with a high IRR as less risky than a low IRR investment. Interest rates for discounting cash flow include a "risk" component and an "inflation" component.
If inflation rates rise during the investment period, or if the appropriate discount rate for NPV rises because of risk considerations, the high IRR investment retains greater NPV than the lower IRR investment. - Analysts view more extended payback periods as riskier than shorter paybacks, only because of the longer time it takes to recover investment funds.
When using the above metrics as decision criteria, however, the prudent investor will attempt to assess the likelihood that returns do appear as projected, as well as the possibility that other better and worse results appear.
IRR is the Same Metric as Yield to Maturity (YTM)
Another reason that IRR is a favorite metric for people trained in finance is that IRR is usually center stage when evaluating bond investments. Note, however, that in bond investment, the same IRR metric carries the name "Yield to Maturity (YTM)."
If the IRR exercises above remind you of something you have seen before—solving an NPV equation for an interest rate—it is likely you are already familiar with the yield to maturity concepts in bond investing. IRR and YTM are mathematically the same concepts, with only a slight difference in definition.
Yield to maturity is the interest rate, "i," that satisfies this version of the NPV equation:
Bond Purchase Price
= FV1/ (1+ i)1+ FV2 /(1+ i )2+...+ FVn /(1 + i )n
This definition for YTM transforms into Definition 1 for IRR, simply by subtracting "Bond Purchase Price" from each side of the equation. Thus, bond purchase price becomes the FV0 in the NPV equation used above for IRR Definition 1. Remember that IRR is the interest rate i that solves this form of the NPV equation:
0 = FV0+FV1/(1+ i )1+FV2 /(1+ i )2+ ...
+ FVn /(1 + i )n
Given the same cash inflows and outflows, the same value of "i" solves both equations. This equality suggests another reason that IRR is popular with financial specialists. IRR serves to evaluate and compare different business investments, even when the investments are quite different.
For in-depth coverage of yield and other bond concepts, see the encyclopedia entry Bond.
Is IRR Appropriate for Lease vs. Buy Decisions?
What Are Other Problem IRR Results?
Analysts can usually find an IRR and interpret its meaning when they analyze a net cash flow stream that has the investment curve profile: Net cash outflows appear very early in the cash flow pattern, while net cash inflows follow through the rest of the life. This profile is typical for some kinds of financial transactions, such as bond investments or bank deposits. The same pattern may also characterize some investments in income-producing assets, or sometimes even the economic consequences of projects, programs, product launches, and other actions.
In many organizations, however, the routine practice—or policy—is to require an IRR estimate for all action proposals, even when expected cash flows do not fit the investment curve profile. Consequently, those who must provide IRR support for their project proposals may react with surprise and dismay when they produce the metric and find any of the following:
- An IRR does not exist for their cash flow stream
- Multiple IRRs exist for a single stream
- There is a negative IRR
- One proposed action shows an IRR 10 or 20 times larger than a competing option.
In such cases, IRR is not appropriate for evaluating the investment or action.
Lease vs. Buy vs. IRR
When the Lease option in a "Lease vs. Buy" comparison involves a typical operating lease, the two net cash flow streams in view have these characteristics:
- The "Buy" option starts with a high initial cash outflow for the asset purchase. In the remaining years of the purchased asset's life, it should earn returns, leading to positive net cash flows in most periods.
- The "Lease" option for the same asset starts with a minimal initial cash outlay (if any) for the first period. Periodic net cash flows for subsequent periods should be almost the same as the net returns under the "Buy" option, but slightly less due to the periodic leasing fees.
The two cash flow streams in Table 5 fit this pattern. The "Buy" stream has an IRR of 42.6%. And, the "Leasing" option has an IRR of 1,400.0%. Imagine choosing between these two options using IRR as the sole decision criterion!


In fact, when results of this kind appear, most people immediately ask: "What's wrong with this picture?" Here are three of the problems:
What's wrong with this IRR picture?
- The analyst can rightly refer to the Buy option as an "investment." A better description of the Lease option is a 7-year "commitment to a service contract with periodic fees." The two profiles differ substantially from each other. Note that the Lease profile is not an investment curve.
- IRR looks only at the net cash flow figures each year. The more substantial inflows each year "mask," or "hide" the leasing costs from IRR.
Some analysts may compare these investment options with the Simple ROI metric, in preference to IRR. Simple ROI is sensitive to the sizes of periodic cash inflows and outflows. Note especially that both options have precisely the same ROI, that is, 226% - Both IRRs are indeed much higher than the company's real cost of capital and real earnings rates for returns, especially the Lease option IRR.
The analyst who still insists on taking an "investment" view of both options should probably turn instead to the modified internal rate of return MIRR. Here, MIRR for the Buy option is 22.5%, while MIRR for the Lease option is 99.3% (basing MIRR on an 8% earnings rate for returns).
As a result, "Lease vs. Buy" decisions that turn entirely on IRR values almost always favor leasing as the better business decision. The internal rate of return metric usually prefers "leasing" because IRR views both actions as financial investments. For the Lease vs. Buy decision, however, decision-makers may consider factors other than IRR as more critical, such as the impact on the company's asset base, tax consequences, and flexibility to upgrade or replace assets.
Negative, multiple, and Impossible IRRs
For some cash flow streams, it is mathematically possible to produce negative IRRs, or several IRRs (more than one discount rate that leads to a 0 NPV for a single cash flow stream). Also, for other cash flow streams, there is no mathematically correct IRR solution.No IRR Solution
- There are many possible cash flow stream profiles that for which there is no IRR solution.
- Firstly, there may very well be real cash outflows and actual cash inflows every period, but when the inflows always outweigh outflows, net cash flow is therefore positive every period. Thus, cash flow streams with positive net cash flows only, do not have an IRR solution.
- Secondly, when cash outflows outweigh cash inflows every period, net cash flow every period is negative. There is also no IRR in such cases.
- Some other cash flow stream profiles that include both negative and positive periodic net cash flows, for which an IRR solution is still impossible.
Multiple IRRs
-
A net cash flow stream tha thas several IRRs or more when it includes more than one sign change in the net cash flow figures.
- When the first periodic net cash flow is negative and the second net cash flow is positive, that is one change of sign. And, If there are no more changes of sign in later periods, there will be no more than one IRR for the stream.
- If there comes another, later, net cash flow event that is negative, that makes two changes of sign. There can, in fact, be one IRR for every such change in the cash flow stream. Therefore, a cash flow stream with four such changes may have up to four IRR values.
- When multiple IRRs exist for a single stream, analysts may choose to refer to the IRR closest to the real cost of capital as the "true" IRR.
Negative IRR
- It is also possible for some net cash flow streams to produce a negative IRR value.
- When the stream of net cash flow figures leads to a negative IRR, the analyst may consider the investment or action a "net loss."
- Further quantitative analysis of negative IRRs, however, is almost always meaningless.
- Analysts should disregard negative IRRs when preparing IRR averages, or weighted average IRRs for multiple actions.
Using IRR: The Four Commandments
The IRR outcomes and problems above suggest four rules, or "commandments" for IRR usage:
- IRR is not appropriate when the net cash flow stream differs substantially from the profile with early-arriving net cash outflows and later net cash inflows.
- Do not use IRR to compare competing cash flow streams whose profiles differ substantially from each other.
- The analyst should not over-interpret IRR magnitude and return rates when IRR differs substantially from the real cost of capital and real earnings rates for returns.
- Do not expect to find an IRR when the net cash flow stream is entirely positive or entirely negative because there is no IRR for such situations.

