What Are Bonds and Bond Investing?
Companies and governments issue bonds (create debt) to borrow funds for present use.
For much of the investment community, bonds are the primary alternative to stock market investments. Bond investments differ from stock share investments regarding the factors that drive investment returns and risks.
Define Bond
A bond is a written promise to repay borrowed money with interest at some future date, usually several years or more after the date of issue.
For the bond issuer, the bond is a debt, or liability. For the bondholder, the same bond is an asset, usually considered an investment.
Bonds are also called notes, bills, or debt securities. Any of these terms may represent these instruments on the Balance sheet, for instance.
Modern usage of the term bond in finance remains true to its origins in medieval English. Since the 14th century, "bond" has meant a binding covenant or agreement, where one party is legally bound to pay a sum to another.


Why Do Companies and Governments Issue Bonds?
Companies and governments issue bonds (create debt) to borrow funds for present use. And, investors buy and sell this debt to earn interest and possibly benefit from changes in their market prices.
The issuer agrees to pay interest at a particular rate (percentage of bond face value) and then repay the principal at the end of bond life when it reaches maturity. As a result, bond investments have very different market price dynamics from other kinds of securities such as stock shares. Because investors know ahead of time the amounts and timing of future interest payments, bond prices rise or fall when prevailing interest rates change (see the section Yield, below).
When a firm issues bonds, the debt appears as a liability on the issuer's Balance sheet. And, when companies invest in bond debt issued by other companies, the debt appears on the bond-holding firm's Balance sheet as an asset (See Balance sheet example, below).
Note in the following sections that various classes of bonds that differ concerning the timing of interest payments as well as owner options and issuer options during their lives.
Explaining Bonds and Bond Investing in Context
Sections below further explain the role of bonds in debt financing and investing in context with related concepts and example calculations. This article explains…
- Principles of bond debt financing in context with bond-relevant terms including: par value, maturity, premium pricing, junk bonds, bearer bond, convertible bond, put provision, call provision, floating rate bond, book-entry system, and registered bond.
- Basic principles and core terms of bond investing such as: face value, basis points, market value, interest, coupon, zero-coupon bond.
- Bond calculations with examples, including the bond yield curve, current yield, and yield to maturity YTM.
- Illustrates bond rating systems, including Moody's Ratings, Standard & Poor's, and Fitch Ratings.
Contents
- What are bonds and bond investing?
- Bond purchase terms.
- Which factors influence bond prices?
- Understanding bond interest payments.
- Special provisions protect investors and issuers: Call, put, and conversion.
- What is "bond yield?" How do investors measure bond yield?
- Understanding bond yield mathematics.
- Understanding discount and premium pricing.
- Understanding yield curves and interest rates.
- Which companies and governments issue bonds?
- What are bond ratings? How are bond ratings interpreted?
- Balance sheet example: Debt and assets.
Related topics
- For a more comprehensive view of balance sheet debt, including bond debt, see the article Liability.
- The role of bond debt and other debt in creating leverage is the subject of the article Capital and Financial Structures.
Bond Purchase Terms
Several common terms have special meaning when they refer to bond purchase, including "par value," "source," and "price."
Par Value
The bond's par value, or face value, is the amount that the issuing company or government entity promises to repay the holder at a specific date (maturity date). A "$100 Bond" has a par value of $100, meaning the holder will receive $100 at maturity in addition to any interest earnings.
Source
Investors can buy bonds (like shares of stock) directly from issuing entity. However, they can also buy and sell bonds and stock shares in secondary markets. For "bonds," these are called bond markets or, equivalently, credit markets or debt markets
When investors buy bonds in the secondary market, of course, the purchase price goes to the previous bondholder, not the issuer.
Price
The bond price is the price investors pay to purchase a bond, whether they buy directly from the issuing entity or buy in the secondary market
Factors Influencing Bond Prices
The Roles of Prevailing Interest Rates and Issuer Credit Rating
When the investor buys a new bond issue directly from the issuing company or government entity, the selling price is usually close to its par value (face value). During its life, however, the market price can and probably will fluctuate, depending on several factors.
Bond Price Depends on Prevailing Interest Rates
Rates that may affect prices include especially current interbank lending rates, government lending rates, inflation rates, and interest rates that competing investments are paying.
Bond prices fall when interest rates rise. Because most bonds pay interest as a percentage of their original (par) value, a lower price effectively gives the new purchaser a higher return rate (relative to the new purchase price), comparable to prevailing interest rates. On the other hand, when prevailing interest rates fall, bond prices typically rise for reasons based on the same dynamics.
Bond Prices Depend on the Issuer's Credit Rating
If the market believes that repayment at maturity from this issuer (lender) is at risk, the issuer's bond rating suffers and market price declines. When investors see a higher risk of repayment from an issuer, the issuer must offer higher interest rates to attract buyers. As a result, risky companies are said to have a higher cost of capital or higher cost of borrowing.
Note that very high-risk bonds are sometimes called, unkindly, junk bonds. These bonds pay interest at extremely high rates, but everyone involved understands that the high returns come with a high risk of default. Default occurs when the issuer is unable to make interest payments on time.
Bond Prices Depend on Current Economic Conditions
Bond prices may also change when investors expect changes in the health of the issuer's industry segment.
Understanding Bond Interest Payments
How is Bond Ownership Registered?
When investors buy bonds in the secondary market, of course, the purchase price goes to the previous bondholder, not the issuer. As an exception to this, however, see the description of zero-coupon issues below.
Bearer Bonds and Coupons
Through most of the twentieth century, bond issuers printed certificates with many "coupons" attached. When an interest payment was due the bearer, the bearer simply "clipped" a coupon and sent it to the issuer. Securities of that type are known as "bearer bonds," because the person with physical possession of the certificates receives payments. Not surprisingly, many owners during this period kept their bond certificates in safe deposit boxes.
Registered Bonds
In the early 1980s, issuers began the transition to registered bonds which have print the owner's name on the certificate. With registered bonds, issuers send regular interest payments to registered bondholders automatically. When "registered" securities trade, of course, the ownership change must be registered with the issuer.
Book-Entry System
More recently, issuers have further transitioned to the so-called Book Entry system. With this system, issuers send interest payments directly to the bond holder's account with a financial institution.
Now, in the 21st century, printed paper coupons have all but disappeared from these investments. Nevertheless, many still use the terms coupon-paying bond and coupon rate. Note that coupon rate is an interest rate, a percentage of par value that issuers pay periodically to holders.
Zero-Coupon Bonds
Zero-coupon bonds earn interest but do not pay it during their lives. Instead, the zero coupon bondholder receives a single payment at maturity, to cover interest earnings and repayment of the original face value price. As a result, for zero coupon securities, the purchase price at the start of bond life is well below the total payment at maturity.
Many people first meet zero coupon securities in the form of saving bonds such as government-issued "savings certificates." Note that US government savings certificates are different from US Treasury issues, which do pay interest at a fixed rate every six months until maturity.
For instance, a 10-year zero coupon bond with a face value of $10,000 should sell for about $4,564 at the start of its life. This estimate assumes an 8% annual interest rate and payment of $10,000 to the holder ten years later at maturity. Note that $4,564 is the present value for a future value of $10,000, with a discount rate of 8% with semiannual compounding for ten years.
For a complete explanation of these terms, see Time Value of Money in this encyclopedia. For working spreadsheet examples of the calculations, see Financial Metrics Pro.
Interest Rate
Fixed rate bonds pay interest, usually semiannually, as a fixed percentage of face value. A $10,000 issue paying 8%, pays interest to the bondholder of $400 every 6 months, for instance. These semiannual installments make a total annual interest payment of $800, or 8% of face value.
This percentage, however, describes the holder's return rate only if the holder bought the security at par value. The term yield refers to the holder's actual return rate, based on the actual purchase price, and other factors. For more on this concept, see the following section, Yield.
Most bonds currently in trade are either (a) fixed rate coupon paying issues or (b) the zero coupon variety. Note, however, that floating rate bonds are also available to investors, for which the interest rate is adjusted periodically to align with a standard interest rate index such as interest rates on US Treasury bills.
What Are Call, Put, and Conversion Provisions?
How Do Provisions Protect Investors and Issuers?
Bonds imay have special provisions at the time of issue, that give either the issuer or the investor options for ending the life of the security.
The Call Provision
Bonds with a call provision allow the issuer to redeem the debt at a specified date and price before maturity. The issuer may decide to exercise the call provision if interest rates decrease substantially and borrowing at a much lower rate becomes possible.
The call provision protects the issuer, but at the same time, it provides increased risk for the investor. These securities, therefore, usually compensate the investor by paying interest at higher rates than comparable securities without the provision.
The Put Provision
Bonds with a put provision allow the holder to sell the security back to the issuer at a given price and date. The holder may want to exercise the put option to bring in cash. Or, the bondholder may especially wish to apply the put provision after interest rates rise, and then reinvest the funds at a higher interest rate.
As a result, the put provision protects the investor but increases the risk to the issuer. These securities, therefore, compensate the issuer by paying interest at lower rates than comparable securities without the put provision.
Convertible Ponds
Some corporate debt issues give the issuer the option to convert them into common stock shares instead of paying interest to holders. This provision is known as a conversion option, and the securities are called convertible bonds.
The convertible securities generally pay interest at lower rates than comparable non-convertible securities because they offer the investor the possible advantages of stock ownership.
What is Bond Yield?
How Do Investors Measure Bond Yield?
The yield concept provides a common bond metric that lets investors compare securities of different kinds and maturities, regarding the returns they offer. The coupon rate (previous section, above) describes interest payments based on the face value. Yield figures, however, represent the effective return rate to the investor, taking into account the actual bond purchase price, future interest earnings, and (in the case of yield to maturity) the issuer's face value repayment at maturity.
The reason that investors turn to yield metrics, in addition to the coupon interest rate, should become clear after considering the following example.
- Consider for instance an investor who buys a bond with an 8% coupon rate and a face value of $10,000.
- Suppose also the investor buys the bond in the secondary market for $8,500.
Even though the investor bought the bind for $8,500, it still returns $800 in interest each year (8% of the par value, $10,000, paid in $400 increments twice yearly). These figures suggest that the investor's $8,500 purchase is gaining an "effective" return somewhat above 8% of the purchase price. But what is the real, effective return rate? That is, what is the yield? What is the percent yield formula?
Two primary approaches to yield calculations attempt to answer these questions: Firstly, Current yield and, secondly, Yield to maturity (YTM).
Basis Points vs. Percentages
Note in the examples below, by the way, that yield figures are percentages, but yields also appear as "basis points."
- A basis point is 1/100 of 1%.
- A yield of 8% is also, therefore, a yield of 800 basis points.
What is Bond Current Yield?
Understanding the Most Straightforward Bond Metric
The Current yield for a bond is merely the annual interest payment, as a percentage of the purchase price. Current yield does not consider any gains or losses for the investor when the purchase price and face value payout at maturity are different.
Consider, for example, a purchase with these characteristics:
• Face value (par): $10,000
• Maturity: 10 years after issue
• Interest rate (coupon rate) paid: 8%
• Interest payment: semiannual (2 times per year)
What is Current Yield When Price Equals Par?
For the investor who buys at face value (par), the current yield and coupon rate are the same. When buying a $10,000 security for $10,000, with a coupon rate of 8%, the bond provides $800 interest annually. The investor's annual return as a percentage of the investment (current yield) is 8%.
What is Current Yield When Price is Below Par?
If the investor buys the $10,000, 8% security in the example above at a market price of $8,500, it will still pay $800 per year interest. As a result, this makes a current yield of $800 / $8,500, or 9.4% (940 basis points).
A drop in the price below par would likely occur, for instance, if interest rates in the economy in general rise. Now, only at the below-par cost does the bond offer investors return rates that compare favorably to new, higher rates available with other potential investments.
What is Current Yield When Price is Above Par?
If the $10,000, 8% instrument has a market price of $11,000, current yield is $800 / $11,000, or 7.3% (730 basis points).
An increase in price above par will likely occur if interest rates in the economy fall. Now, at the higher price, the bond offers investors return rates comparable to new, lower rates available on other potential investments.
Bond Yield to Maturity YTM
Understanding the Preferred Metric for Comparing Bond Investments
Investors considering different bond investments typically prefer to compare potential investments using the Yield to Maturity (YTM) metric. YTM is the metric of choice because investors know it considers all of the following:
- Firs, the purchase price of the bond
- Second, the bond's par value, which the investor receives at maturity
- Third, all interest earnings during the holder's ownership
The YTM calculation is more complex than the current yield calculation above because it involves time value of money concepts
Upon first hearing the YTM concept, investors often ask how to make practical use of YTM results. They find, unfortunately, that financial experts may be quick to define YTM but many are not so ready to explain YTM usage.
Defining Yield to Maturity as the Cousin to Internal Rate of Return IRR
Analysts define yield to maturity as the discount rate (interest rate) that equates (1) bond purchase price with (2) the present value of all future interest payments and face value repayment. For the example bond in the previous section, ($10,000 par, 8% coupon rate, semiannual interest payment), with purchase price of $8,500 and 6 years remaining to maturity, the percentage that equates (1) and (2) above is Yield to Maturity, 11.5%.
At this point, those with a background in finance may begin to suspect they have seen something like this definition before. The sense of deja vu is appropriate because YTM is just the cash flow metric internal rate of return (IRR) under a different name.
To see why YTM and IRR are practically the same metrics, consider first the above definition as a written equation:
YTM is the interest rate for which:
Bond Purchase Price = Present Value of All Future Cash Inflows
Internal return for the same bond investment is just a simple rearrangement of the above equation. IRR is the interest rate (discount rate) that equates both sides of this equation:
0 = Bond Purchase Price – Present Value of All Future Cash Inflows
For a proposed bond investment, therefore, IRR for the investment is the same as the YTM for the investment. The section below "Understanding Bond Yield Mathematics" presents more on the mathematical basis of YTM and IRR.
Interpreting Yield to Maturity in Practical Terms for Investors
YTM —like other cash flow metrics such as Payback Period, ROI and NPV—takes an "investment view" of investment cash flow results. Each compares the timing and magnitude of investment gains to investment costs. And, each metric has its unique way of making this comparison. In any case, businesspeople should understand firstly, which conclusions about YTM numbers they can rely upon without further justification.
- If YTM for a possible bond investment is higher than the investor's cost of capital, the investment is a net gain.
- When YTM for a possible bond investment is less than the investor's cost of capital, analysts generally regard it as a net loss.
- When using YTM to compare competing investment opportunities, other factors being equal, the investment with the higher YTM (or IRR) is preferred.
YTM Conclusions That May or May Not be Reliable
Investors sometimes draw still other kinds of conclusions about YTM numbers. Investors should understand, however, that these conclusions may or may not be justified. They may ask, for instance, "Is a bond investment with YTM = 12% twice as profitable as an investment with YTM = 6%?
The answer to that question requires more analysis using (a) the investor's real cost of capital, (b) the actual return rate the investor achieves on re-invested funds, and (c) accurate estimates of future interest rates. The article "Internal Rate of Return" introduces and explains this kind of YTM reasoning.
The next two sections show the mathematical basis for this result, and another section further below, "Discount and Premium Pricing," explains how the relationships between yields and coupon rates change when interest rates change. To skip the next mathematics sections and go directly to the following topic on YTM for Zero-Coupon securities, click here.
Understanding Bond Yield Mathematics
Yield is All About the Investors Cash Flow Stream
For the following example, yield to maturity is an interest rate that equates the purchase price with the present value of all future inflows from the investment. YTM is based on the same bond and transaction characteristics as the current yield calculations above, except that YTM also factors in the time remaining until maturity.
Face value (par): $10,000
Purchase price: $8,500
Coupon rate paid: 8%
Maturity: 10 Yrs after issue
Time to maturity at purchase: 6 years
Interest payment frequency: 2 times/year
Bond Cash Flow Stream in Chart Form
Graphically, the cash flow stream for this investment looks like the stream in Exhibit 1 below.
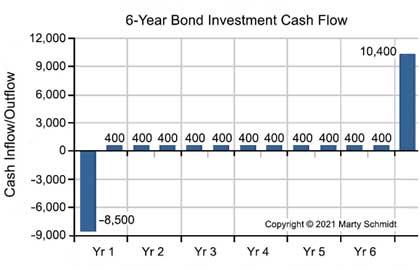
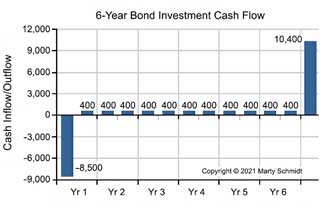
Defining Yield to Maturity
Yield to maturity, then, is the interest rate that creates a net present value of all the cash inflows (to the right of the one cash outflow) equal to $8,500 (see the article "Time Value of Money" for complete coverage of these concepts). Note that twelve interest-paying periods occur between purchase and maturity (twice yearly payments for six years), and the interest rate for each is the annual rate ( i ) divided by 2. YTM is then the value of i that solves this equation:
8,500 = 400 / (1+i / 2 )1 + 400 / (1+i / 2 )2 + ... +400 / (1 + i / 2 )11 + 10,400 / (1 + i / 2 )12Looking ahead, we will find that an annual interest rate ( i ) of 11.5% solves this equation. 11.5% is the yield to maturity for this investor. (1150 basis points).
A Graphical Solution for YTM
In fact, there is no known analytic solution for the above equation so that spreadsheets and other software find the interest rate by "trial and error" (more accurately, they use "successive approximations"). The program calculates NPV with different discount rates, compares the result with the price to be matched, adjusts the discount rate for the next calculation, and so on until it finds a value that satisfies the equation.
You can get a sense of how this works from Exhibit 2, which shows the NPV (sum of present values) of the cash inflows in the chart above, at different discount rates (different i values).

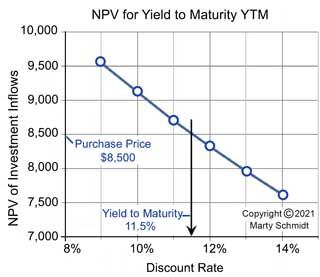
The Role of the Standard NPV Formula in YTM
For Exhibit 2 above, the NPV curve results from the standard NPV formula in Exhibit 3, below.


For example, set NPV = 8,500, and set FV0 equal to 0 (in other words, there is no immediate interest payment). Let all the other FVs from FV1 through FV11 equal 400 (semiannual interest payments are
"future values" in the discounting calculation). Let FV12 equal 10,400 (the final interest payment plus par value repayment), and let q
= 2 (the number of interest periods per year). The value of
"i" that satisfies the equation, in this case, is 11.5%.
YTM vs. Internal Rate of Return (IRR)
If the exercise above looks familiar to you—solving an NPV equation for an interest rate—it is likely that you are already acquainted with another investment metric, the "Internal rate of return" (IRR). IRR and YTM are mathematically the same concepts, with only a slight difference in definition.
Once more, remember that YTM is the interest rate i that satisfies this version of the NPV equation:
Purchase Price = FV1 / (1+i / 2 )1 + FV2 / (1+i / 2 )2 + ... + FVn / (1 + i /2 )n
The definition formula for IRR moves "Purchase Price" to the other side of the equal sign. This move creates an immediate cash outflow, the FV0 in the equation. The definition formula then asks for the same "i" that solves the equation:
0 = FV0+ FV1 / (1+i / 2 )1 + FV2 / (1+i / 2 )2 + ... + FVn / (1 + i /2 )n
Given the same cash inflows and outflows, the same value of "i" solves both equations. The YTM and IRR equations, in other words, are merely different forms of the same equation. This is probably one reason that people with financial backgrounds often turn to IRR, when comparing potential business investments. They do so even when the comparing investments of quite different kinds. The projected IRR for, say, an investment in a marketing program compares directly with the YTM of a potential bond investment.
Yield to Maturity Metric YTM for Zero-Coupon Bonds
Zero-Coupon Bond Prices Change as Interest Rates Change?
For zero coupon bonds (which pay interest and principal in a single payment at maturity), the yield to maturity concept is the same concept that appears in the example above. With zero-coupon bonds, however, the idea is easier to apply. Here, there is only one present value cash flow to equate with the purchase price, namely, the face value payout at maturity.
Examples show how YTM calculates for zero coupon bonds under several conditions.
Zero-Coupon When First Issued
Consider the YTM for the 10-year zero-coupon bond from an example in the previous section.
- This bond has a face value of $10,000 but sells at the start of its life for $4,564.
- The YTM for this bond is 8% (800 basis points). This YTM is merely the discount rate that equates the present value of the future payment ($10,000) with the amount of the initial purchase price ($4,564).
Zero-Coupon Price After Interest Rate Decrease
Consider the same zero-coupon security, now four years into its life with six years remaining until maturity. Suppose its market price at this time is $8,500. What is its yield to maturity?
- YTM for this bond is the annual interest rate that brings the present value of a $10,000 payment down to $8,500, after 12 semiannual compounding periods (6 years).
- The semiannual interest rate that does this is 1.35% which, on an annual basis is a 2.7% YTM (280 basis points).
The decrease in YTM (compared to the original YTM) would likely result if interest rates in the economy, in general, had fallen.
Zero-Coupon Price After Interest Rate Increase
Consider the same zero coupon security four years into its life, with six years remaining until maturity, but now selling at a market price of $5,500. This price is slightly above the initial par value purchase price ($4,564), but the security is now only six years from maturity. And, as maturity nears, a bond that maintains a constant yield will see its price move closer to par value. Now, what is its yield to maturity?
- An interest rate (discount rate, or yield to maturity) of 10.3% creates a present value of $5,500 for a $10,000 payment five years away.
- The rise in YTM over its initial value would occur if interest rates in the general economy had similarly risen.
When Interest rates rise, the security sells at a lower price.
How to Find Bond Yields With Microsoft Excel
Spreadsheet Solutions for Yield Mathematics
Current yield calculates as a ratio of two numbers, the periodic interest payment amount over the purchase price. However, Yield to maturity is "found" rather than calculated, by trying different interest rates until a rate appears that equates purchase price with the present value of all future payments to the investor.
Finding YTM values could be a cumbersome, work-intensive exercise, except that today the internet provides an abundance of easy-to-use yield calculators. Most pre-programmed financial calculators also find YTM from a simple entry of data.
Alternatively, Microsoft Excel YIELD functions provide a fast and easy way to find YTM. A single Excel function, YIELD, can deliver yield to maturity for both coupon paying investments and zero coupon securities.
Example:
YTM for a Coupon Paying Investment with Excel YIELD Function
The first example below re-uses data from above to show how Excel YIELD function finds yield to maturity for a bond transaction with the characteristics shown here. Bold terms are Excel names for YIELD function input parameters.
Face value (par): $10,000
Pr (Purchase price): $8,500
Coupon rate paid: 8%
Maturity: 10 yrs after issue
Time to maturity at purchase: 6 years
Interest payment frequency: 2 times/year
The Excel YIELD function
Excel produces Yield to Maturity with the function
YIELD(settlement, maturity rate, pr, redemption, frequency, basis)
Using the example data, the cell that is to show YTM will look like this:
=YIELD(DATE(2010,10,1),DATE(2016,10,1),0.08,85,100,2)
The spreadsheet user should see the resulting YTM of11.5% in the cell. Notice the following about the input parameters,
- Date entries here use the Excel DATE function. For settlement date, 1 October 2010, the user could have entered the sequential number Excel uses to store and manipulate dates (the default for that date on a Windows PC is 40452). However, it is clearer and easier to let Excel find the number through the DATE function, that is, by entering DATE(2010,10,1).
- Users enter coupon rate either as a decimal fraction (0.08) or as a percentage (8%). Percentage entries should include the % sign. For the YIELD function, enter the annual coupon rate.
- Users enter Purchase Price (Pr) and Redemption value (face value) as units per 100. The enter a price of $8,500 as Pr of 85, and $10,000 redemption value as 100.
- For most purposes, users can omit the basis parameter (thereby choosing the default setting). For those who wish to use it, basis allows for slightly different ways of calculating interest, e.g., 30 day months and 365 day year, vs. a 360 day year and so. The Excel Help System explains more on this.
Example:
YTM for Zero-Coupon Security with Excel YIELD Function
The only difference between the example above for a coupon paying investment, and the next example for zero-coupon security, is the use of the rate parameter. Zero coupon bonds pay no periodic interest during their lives, and so a "0" is entered for the YIELD function's rate parameter. Here again are similar data, but this time for zero coupon investment:
Face value (par): $10,000
Purchase price: $8,500
Coupon rate paid: 0%
Time to maturity at purchase: 6 years
Interest payment frequency: 2 times/year
The spreadsheet cell that displays YTM for this zero-coupon investment has this formula:
=YIELD(settlement, maturity, rate, pr, redemption, frequency, basis)
=YIELD(DATE(2010,10,1),DATE(2016,10,1),0.00,85,100,2)
The spreadsheet user sees the YTM value of 2.7% in the cell. Notice that the YIELD function requires a non-zero coupon frequency, the final parameter to enter here, even when the coupon rate is 0. Entering a frequency of 0 produces an error message.
Bond Yield Curves and Interest Rates
What Do Different Yield Curve Profiles Indicate?
The examples above show that as interest rates in the economy rise and fall, bond prices also fall and rise in response. As a result, investors have a keen interest in forecasting future interest rates and interest rate changes. And, like all investors, they have a keen interest in understanding the risks in their investments. For investors, a yield curve is a central tool for interest rate analysis and risk management.
Some investors view the yield curve very much in the way that so-called technical analysts see stock price charts. This approach assumes that historical displays contain information that helps predict future price and interest changes. Others view the curves just as a description of what the market expects interest rates and costs to do in the near and long-term, and a tool for balancing risks against rewards.
A Typical Yield Curve
A typical yield curve for debt securities of a given class might have the form of the curve in Exhibit 4.

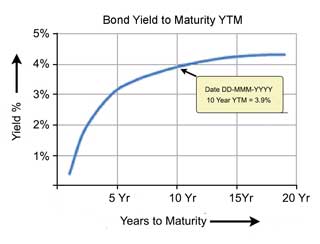
Plotting points for the curve in Exhibit 4 represent a number of bonds of approximately equal credit quality, but different maturities. The horizontal axis represents the number of years remaining until maturity and the vertical axis represents bond yield as a percentage. Each such curve represents YTM values for these bonds as they stand on a specific date.
To investors and analysts, the chart's message conveys in its shape. In this example, for instance, longer maturity securities have a higher yield compared to shorter. Investors ordinarily expect this difference because it is reasonable to view longer maturities as riskier, and therefore having to pay higher yields. In any case, three main classes of yield curve shapes are:
- "Normal" yield curve (Exhibit 4 and Exhibit 5 below): In these curves, shorter-term instruments have lower yields, and longer-term bonds have higher yields.
- "Inverted" yield curve:In these curves, longer-term instruments have shorter yields, shorter-term instruments have higher yields. Investors understand this to mean that a recession is forthcoming (or at least, the market expects a "recession").
- "Flat" curve, or "hump" curve: Relatively longer and longer-term bonds have similar yields. Medium-term instruments may not have different returns. In either case, this would indicate that the market expects some economic transition.
Yield curve "slope" also carries a message: A steep slope indicates a rapid change in interest rates, but a shallow slope suggests the opposite.
Example US Treasury Note Yield Curve
All three yield curve shapes can be present in the same economy, at the same time, depending on the credit quality, issuing source, and nature of the payment schedule. Yield curves, moreover, change daily for some securities. The US Treasury, for instance, publishes yield curve data for US Treasury notes on a daily basis1.
Exhibit 5 below shows 3 daily examples from different years.

Notice in Exhibit 4 that investors purchasing 30-Year US treasury notes in 1990 "locked in" a yield of 8.84% through 2020, even though interest rates in general declined substantially during that period. New 30-year notes purchased in 2020 are now paying interest with a yield of 2.2%, "locked in" for the next through 2050. One reason that some investors prefer investing in bonds, is that yield rates stay constant throughout the life of the bond, regardless of what happens to interest rates in the general economy.

_______________________________
- Exhibit 5 curves are plotted from US Treasury yield curve data, available for each day from 1-January-1990 to the present on https://www.treasury.gov/resource-center/data-chart-center/interest-rates/Pages/TextView.aspx?data=yield.
Which Companies and Governments Issue Bonds?
How Do They Back Bond Liabilities?
Corporations, governments, government agencies, and municipalities all issue bonds. The discussion below also describes the class of "asset-backed" bonds. Major issuer categories include:
Corporations
For example, issuers include Ericsson, in Sweden, or General Motors in the United States. The credit quality of corporate issues depends on the financial ability and financial prospects of the issuing company.
Supranational Agencies
One such issuer, for instance, is the World Bank. Issues from supranational agencies generally have excellent credit ratings because they have the "full faith and credit" backing of the governments that support and sponsor these agencies.
Governments, Government Agencies, and Government Sponsored Enterprises
For example, bond issuers include the United States Government, the Canadian Province of Ontario, or (in the United States) the Federal National Mortgage Association (Fannie Mae).
Government issues generally have excellent credit quality ratings, because they have the "full faith and credit" backing of the issuing government. Note, however, that debt belonging to the US State of California is an exception to this rule. During two years of financial uncertainty for the state, 2009-2010, the state's credit rating varied between A- and BBB.
Municipalities
For example, bond issuers include the city of Newark, New Jersey, and the city of Toronto, Ontario. Governments sometimes help cities lower the cost of borrowing, by allowing them to sell "Tax-free" notes, from which investors do pay taxes on interest earnings. Tax-free municipal bonds thus pay lower interest than comparable securities without the tax exemption. For investors, however, the tax savings compensate for the lower interest payments.
Mortgage-Backed / Asset-Backed / Collateralized Debt Obligations
These debt securities originate through a process known as securitization. Securitization occurs when a financial institution such as an auto finance company or credit card provider turns its loans into marketable securities.
Bond issuers back these bonds with assets, such as auto loan receivables or credit card receivables. Securities in this class generally have excellent credit quality ratings (usually AAA), because they have the backing of sources other than the loan originator.
What Are Bond Ratings?
How Do You Interpret Bond Ratings?
| S&P Rating |
Description |
|---|---|
| AAA | Prime |
| AA+ | High Grade |
| AA | |
| AA– | |
| A+ | Upper Medium Grade |
| A | |
| A– | |
| BBB+ | Lower Medium Grade |
| BBB | |
| BBB– | |
| BB+ | Non-Investment Grade Speculative |
| BB | |
| BB– | |
| B+ | Highly Speculative |
| B | |
| B– | |
| CCC+ | Substantial Risks |
| CCC | Extremely Speculative |
| CCC– | In Default with Little Prospect for Recovery |
| CC | |
| D | In Default |
Exhibit 6.Standard and Poor's bond rating categories. Rating systems by Moody's and Fitch's are very similar."
Investors and market analysts consider the creditworthiness of issuers carefully. A bond is a debt to repay, after all. When there are uncertainties about the issuer's ability to repay at maturity, or even pay interest before then, the issuer must pay higher interest rates to sell debt. So-called junk bonds are an extreme illustration of this principle: these pay exceptionally high-interest rates but at the same time carry a significant risk of non-payment.
Bonds are given grades, or creditworthiness ratings by independent rating services such as Standard & Poor's, Fitch, or Moody's. The table below shows Standard & Poor's rating system for Tax-free issues, from highest creditworthiness (top) to lowest (bottom). AS&P uses a similar but slightly different set of ratings for short-term bonds.
Bond Rating Systems
The Exhibit 6 table shows Standard & Poor's rating system, but Fitch's approach is nearly identical. Moody's system is also very similar, except that Moody's uses more + and – signs, and lower case as well as upper case letters.
Corporate debt issues (see the previous section, on bond issuers) typically span the range of credit rating levels. On the other hand, government debt, municipal bonds, and asset-backed securities almost always have ratings at the top investment grade levels.
Example Ratings
Among corporate issues, for instance, Microsoft has consistently received an AAA rating. In May 2009 this allowed the company to sell $1 billion in 10-year debt, paying interest at 4.2%.
By contrast, Virgin Media at the end of 2009 had a Standard and Poor's rating of B+, which is "highly speculative" and below investment grade. Virgin Media at that time raised £350 million by selling 10-year bonds and paying interest at 8.75%.
Example Balance Sheet
With Bond Debt and Bond Assets
A company's debt appears on the Balance sheet under Liabilities. In the Balance sheet Exhibit 6 below, note the entry for "Notes payable, short-term" under Current liabilities, and "Bonds payable" under Long-term liabilities.


When a company owns another company's bond issues (debt), bond ownership appears on the Balance sheet under Assets. On this example Balance sheet, note the entries for "Notes receivable" under Current Assets, and "Bonds held" under "Long-Term Investments & Funds."

